Regla de tres …

La regla de tres o regla de tres simple es una forma de resolver problemas de proporcionalidad entre tres valores conocidos y una incógnita, estableciendo una relación de proporcionalidad entre todos ellos.

Es decir, lo que se pretende con ella es hallar el cuarto término de una proporción conociendo los otros tres.

En la regla de tres simple se establece, por tanto, la relación de proporcionalidad entre dos valores conocidos A y B , y conociendo un tercer valor C, se calcula un cuarto valor D.

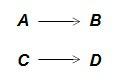
Dicha relación de proporcionalidad existente entre A y B puede ser directa o inversa.

Será directa cuando a un mayor valor de A le corresponda también un mayor valor de B (o a un menor valor de A le corresponda un menor valor de B), y será inversa, cuando a un mayor valor de A le corresponda un menor valor de B (o a un menor valor de A le corresponda un mayor valor de B).

En el primer caso tenemos una regla de tres simple directa, y en el segundo caso una regla de tres simple inversa.

Vamos a ver cada una más detalladamente.

Regla de tres simple directa

Tenemos que:

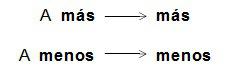
En la regla de tres simple directa, en la relación entre los valores, se cumple que:

y decimos que A es a B directamente, como C es a D.

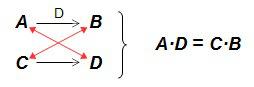
De esta igualdad anterior, se deduce fácilmente que si conocemos los valores A, B y C, y queremos calcular D, éste último será:

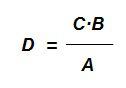
Lo vemos con un ejemplo.

“Una sandía cuesta en el supermercado 4 euros. Juán ha comprado 50 sandías ¿cuánto se habrá gastado?”

Pero… ¿quién compra 50 sandías? ¿las metes todas en el maletero del coche? A no ser que Juán tenga un puesto de frutas en el mercado… ¡se le van a estropear antes de que se las pueda comer todas!

Aprovechando que este fin de semana he estado pintando una habitación, vamos a verlo con un ejemplo algo más real:

“María tiene que comprar pintura blanca para darle una mano previa a una habitación que quiere cambiar de color. Si en el bote de pintura se indica que con 1 litro de pintura se pueden pintar 8 m² ¿cuántos litros necesita teóricamente para pintar las paredes de la habitación si ésta tiene 40 m² de pared?”

En este caso, la relación de proporcionalidad es directa, puesto que cuanto más metros cuadrados de pared tengamos que pintar más litros de pintura necesitaremos. Lo hacemos como hemos visto antes:

María necesitará, por tanto, 5 litros de pintura.

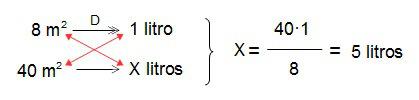
Regla de tres simple inversa

En este caso tenemos que:

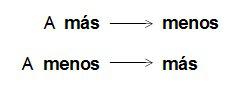
En la regla de tres simple inversa, en la relación entre los valores, se cumple que:

y decimos que A es a B inversamente, como C es a D.

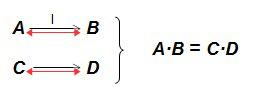
Conocidos los valores A, B y C, el valor D será:

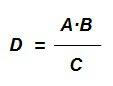
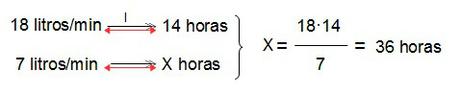
Por ejemplo: “Un grifo con un caudal de salida de agua de 18 litros por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 litros por minuto?”

La relación de proporcionalidad es inversa, ya que cuanto más caudal de salida de agua tiene el grifo menos tiempo (en horas) se necesita para llenar el depósito. Tenemos así que:

Con un grifo de 7 litros por minuto de caudal (menos caudal) necesitamos 36 horas (más tiempo) para llenar el depósito.

Bien, hasta ahora hemos visto cómo resolver problemas de proporcionalidad entre tres valores conocidos y una incógnita, estableciendo una relación de proporcionalidad entre todos ellos y utilizando la regla de tres simple que corresponda, directa o inversa.

Sin embargo, en ocasiones, el problema planteado puede involucrar más de tres cantidades conocidas, además de la desconocida. ¿Cómo hacemos en este caso?

Pues una forma rápida de resolver estas situaciones es utilizando una  regla de tres compuesta.

Una regla de tres compuesta se compone de varias reglas de tres simples aplicadas sucesivamente.

Como entre las magnitudes se pueden establecer relaciones de proporcionalidad directa o inversa, podemos tener distintos casos: que todas las relaciones de proporcionalidad sean directas, que todas sean indirectas, o que se den relaciones directas e indirectas.

Vamos a ver cada uno de estos posibles casos:

Regla de tres compuesta directa

Se aplica cuando todas las relaciones de proporcionalidad que se establecen son directas.

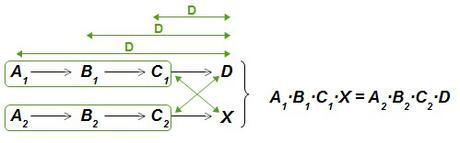
Si conocemos los valores A₁, B₁, C₁, D, A₂, B₂ y C₂,  y queremos calcular X, éste último será:

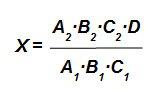
Lo vemos mejor con un ejemplo:

“9 grifos abiertos durante 10 horas diarias han consumido una cantidad de agua por valor de 20 €. ¿Cuál será el precio del vertido de 15 grifos abiertos 12 horas durante los mismos días?”

Primero vemos el tipo de relaciones de proporcionalidad que hay:

Aplicando lo que hemos visto antes, tenemos que:

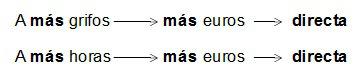
Regla de tres compuesta inversa

Se aplica cuando todas las relaciones de proporcionalidad que se establecen son inversas.

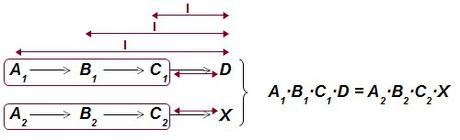
Conociendo los valores A₁, B₁, C₁, D, A₂, B₂ y C₂, el valor de X será:

Por ejemplo: “5 obreros trabajando 6 horas diarias construyen un muro en 2 días. ¿Cuánto tardarán 4 obreros trabajando 7 horas diarias?”

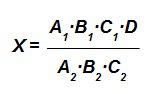
Aplicando la regla de tres compuesta inversa, tenemos:

Regla de tres compuesta mixta

Se aplica cuando en las relaciones de proporcionalidad que se establecen hay relaciones directas e inversas.

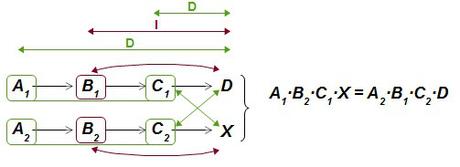
Conociendo los valores A₁, B₁, C₁, D, A₂, B₂ y C₂, el valor de X se obtiene como:

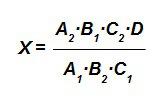
Y, cómo no, un ejemplo, que es como se ve mejor:

“8 obreros han construído en 9 días, trabajando a razón de 6 horas por día, 30 m de muro. ¿Cuántos días necesitarán 10 obreros trabajando 8 horas diarias para construír los 50 m de muro que faltan?”

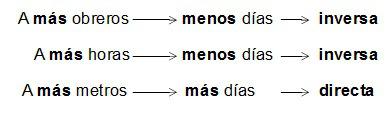
Así que tenemos:

Son más obreros y trabajando más horas al día, pero como también son más los metros de muro que tienen que construir… ¡casualidades de la vida tardan los mismos días!

Está claro que aplicando una regla de tres compuesta el cálculo es inmediato, no obstante, siempre se tiene la opción de ir aplicando reglas de tres simples hasta llegar a la solución que buscamos.

Pues, de esto va la famosa “regla de tres”, algo verdaderamente útil en el día a día.

Imagen inicial de Carlos Rueda.