Pues sí, amiguitos, vamos a hablar de RENFE, pero no de su web (que eso es harina de otro cantar), sino de los descuentos que ofrece en ella.
No, esto no es un post patrocinado (pero si RENFE lo estimara oportuno, uno está abierto a escuchar ofertas.... ¿no? pues nada, sigamos). Vamos a hablar de cómo renfe aplica ciertos descuentos y a darnos cuenta que no es del todo verdad lo que dice.
Vamos a centrarnos en viajes de larga distancia (un AVE Sevilla Madrid, por ejemplo) de ida y vuelta. Tal y como anuncian en su propia web el descuento es del 20%. Pero ¿cómo hacen este descuento?
Uno, ingenuo él, podría pensar que suman el importe del billete de ida y el del billete de vuelta y a esa suma le hacen el 20% de descuento. Lo cierto es que no suelen hacerlo así. En realidad te cobran íntegro el importe del viaje de Ida, y te hacen el 40% en el de vuelta. Yo supongo que esto lo harán por si alguien compra una Ida y, después, decide hacer la vuelta, pero bueno, que tampoco es que lo entienda mucho.
Pero dejémonos de zarandajas y pasemos a las matemáticas. En un principio, a un comprador incauto (o no tato) le podría parecer que ambos métodos son exactamente iguales. Craso error.
Para que ambos métodos arrojen el mismo resultado, el importe de la ida y de la vuelta deben ser iguales. En otro caso, no coinciden.
Vamos a comprobarlo. Supongamos que 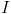 es el importe del billete de ida y que
es el importe del billete de ida y que 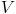 es el importe del de vuelta. Por el primer método explicado (el de hacer un 20% a la suma) tendríamos que pagar
es el importe del de vuelta. Por el primer método explicado (el de hacer un 20% a la suma) tendríamos que pagar 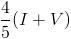 , mientras que por el segundo método (nos hacen el 40% en el de vuelta) tendremos que pagar
, mientras que por el segundo método (nos hacen el 40% en el de vuelta) tendremos que pagar 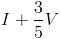 . Para ver cuándo coinciden, sólo hay que igualar y resolver:
. Para ver cuándo coinciden, sólo hay que igualar y resolver: 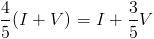 o lo que es lo mismo
o lo que es lo mismo 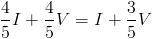 . Si ahora pasamos las
. Si ahora pasamos las 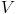 al primer miembro y las
al primer miembro y las 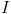 al segundo, se obtiene que
al segundo, se obtiene que 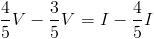 , que en definitiva se reduce a que
, que en definitiva se reduce a que  .
.
Y aquí es donde está la trampa. En muchas ocasiones, es posible comprar billetes de Ida y Vuelta en la que los precios no coincidan (por elegir en unoTurista y en otro Preferente, o bien porque elegimos tarifas diferentes).
En estos casos, ¿qué conviene más? Si usamos el Método RENFE (40% en la vuelta) será más ventajoso siempre que 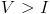 , mientras que si da la casualidad que
, mientras que si da la casualidad que 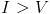 , nos convendría más que nos cobraran el método 1 (20% a la suma).
, nos convendría más que nos cobraran el método 1 (20% a la suma).
En efecto, si 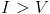 , entonces
, entonces 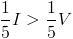 , o lo que es lo mismo,
, o lo que es lo mismo, 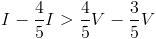 , de donde
, de donde 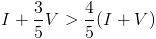 , es decir, si la Ida es más cara que la vuelta, el método RENFE es más caro que hacerte un 20% en ambos trayecto. Por tanto, podrías reclamarles ya que te estarían "timando" ¿no?
, es decir, si la Ida es más cara que la vuelta, el método RENFE es más caro que hacerte un 20% en ambos trayecto. Por tanto, podrías reclamarles ya que te estarían "timando" ¿no?
Así que mi consejo matemático de hoy es que, si después de intentarlo mucho, logras comprar billetes a través de la web de RENFE, procura que el viaje de Ida sea más barato que el viaje de Vuelta, ya que así RENFE te estará haciendo un descuento superior al 20%, por lo que tú serías ahora el "timador".
Para que luego digan que las Matemáticas no sirven para nada. Sirven para "timar" a la RENFE.
Tito Eliatron Dixit
PD aclaratoria: este artículo sólo pretende mostrar una curiosidad matemática relacionada con porcentajes. En ningún momento se pretende desprestigiar a RENFE, ya que, supongo, la forma que tienen de aplicar los descuentos será perfectamente legal y estará escrita en algún lugar de su web (aunque yo, torpe de mí, no lo encentre). El uso de la palabra "timar" se hace de forma entrecomillada para hacer constar lo anteriormente dicho.
PD2: Esta entrada va a formar parte de la VII Edición del Carnaval de Matemáticas cuyo anfitrión será El Máquina de Turing.

