Solución al reto de las 54 cerillas y los cuadrados

Recuerdo lo que decía el reto o problema que proponía:

“Tenemos 54 cerillas (fósforos, cerillos, mixtos, matches…).

Con esas 54 cerillas (fósforos, cerillos, mixtos, matches…) y sin cruzarlas ¿cuántos cuadrados eres capaz de formar?”

Si no lo habías visto hasta ahora o aún no te habías puesto a intentar solucionarlo, intenta resolverlo antes de seguir leyendo.

Si ya has llegado a tu solución (la que consideras mejor) puedes, si quieres, echarle un ojo a la resolución del otro problema de cerillas más sencillo que propuse cuando ví que éste le estaba resultando complicado a la gente: Problema de las 9 cerillas y los triángulos, y quizás te dé alguna idea nueva que no se te hubiese ocurrido.

De una manera u otra, cada persona habrá llegado a una solución, la suya.

Pues bien, vamos a intentar resolver este reto paso a paso, siguiendo más o menos el razonamiento lógico que podriamos llevar hasta llegar a la que considero que seria la mejor solución.

Repito, si no quieres ver aún la solución ¡no sigas leyendo!

RESOLUCIÓN

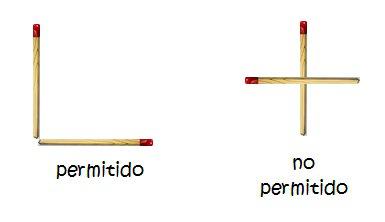
El problema nos dice que tenemos 54 cerillas y que con ellas debemos formar el mayor número posible de cuadrados. Y, además, nos dice que podemos disponerlas tocándose por sus extremos pero no por un punto intermedio (formando una cruz).

Lo primero que se nos podría ocurrir sería formar cuadrados independientes con las cerillas

De esta manera conseguiríamos 13 cuadrados y nos sobrarían 2 cerillas.

Pero al ver la imagen, la idea que se nos viene a la cabeza es “juntarlos”, es decir, utilizar una de las cerillas como lado común

De esta manera empleamos menos cerillas y conseguimos más cuadrados. Concretamente obtenemos así 17 cuadrados y nos sobran igualmente 2 cerillas.

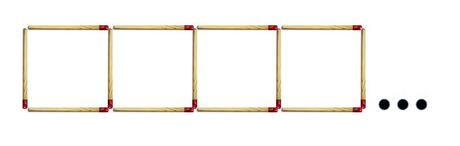
El simple hecho de que nos sobren 2 cerillas a mi personalmente no me gusta mucho, y supongo que a vosotras y vosotros tampoco.

Lo siguiente es pensar: “¿Y por qué no coloco las cerillas de manera que pueda formar cuadrados más grandes?

Es decir, podemos formar, por ejemplo, cuadrados de lado 2 cerillas y que dentro tengan otros cuadrados de 1 cerilla de lado, como se muestra en la imagen siguiente

Así, al haber más cerillas que son lado común a dos cuadrados y además cuadrados de mayor tamaño, conseguimos más cuadrados con el mismo número de cerillas.

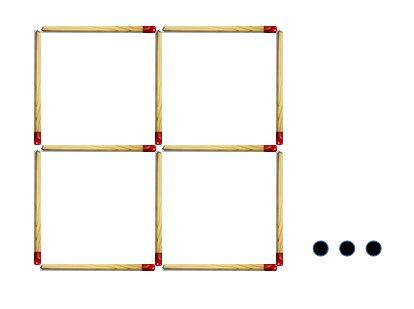
Si esto lo aplicamos a nuestras 54 cerillas, ampliando esta configuración a cuadrados de mayor tamaño, la mejor disposición de las cerillas (habría otras disposiciones equivalentes a ésta) sería la siguiente

Veamos cuántos cuadrados conseguimos así:

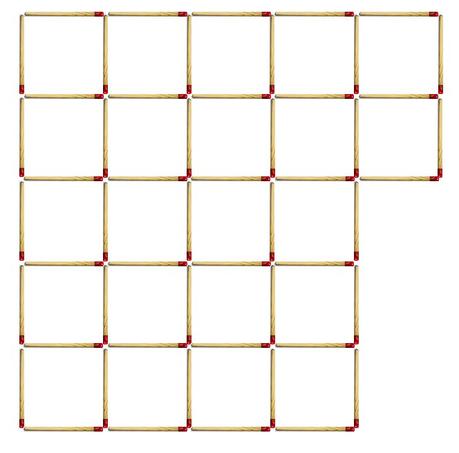
• 22 cuadrados de lado 1 cerilla.

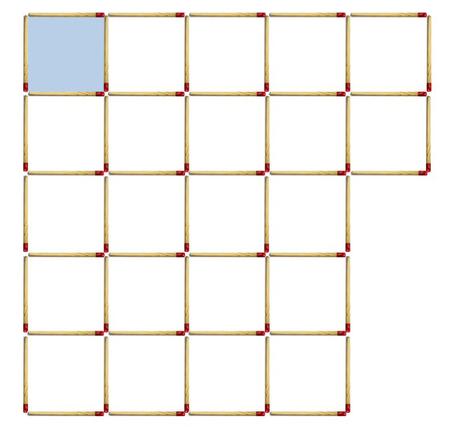
• 13 cuadrados de lado 2 cerillas.

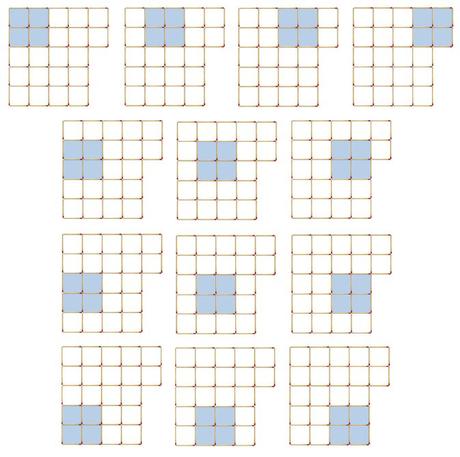
• 6 cuadrados de lado 3 cerillas.

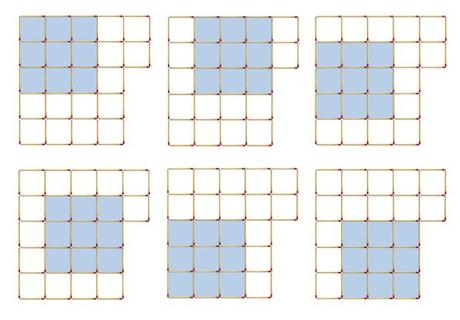
• 2 cuadrados de lado 4 cerillas.

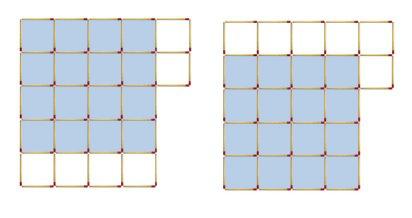
Así que, resumiendo, de esta manera hemos conseguido 43 cuadrados con nuestras 54 cerillas y, además, no nos ha sobrado ninguna.

 ¿Bien no?

¡No está nada mal!

¿Lo dejamos así entonces?

No se vosotros, pero yo no me conformo con esto.

Permitidme que volvamos a la imagen anterior del cuadrado de lado dos cerillas

Lo siguiente que hicimos fué ampliar esta configuración formando más cuadrados alrededor hasta utilizar las 54 cerillas.

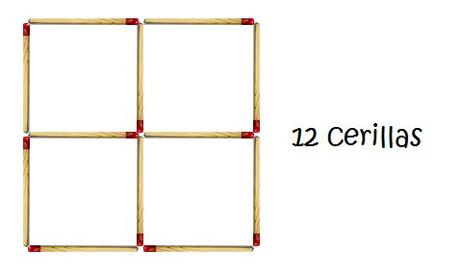
Pero… ¿por qué limitarnos de esta manera?

Puestos a buscar lados comunes prefiero salirme del plano e irme a un espacio tridimensional. Así que seguiré añadiendo cerillas pero perpendiculares a las de antes y cumpliendo la condición que se nos da de que las cerillas deben tocarse en los extremos

y ahora otro cuadrado como el primero
otras tantas cerillas perpendiculares
y, por último, otro cuadrado más
Bien, ya hemos utilizado nuestras 54 cerillas, pero ¿habremos conseguido más cuadrados que de la otra manera?

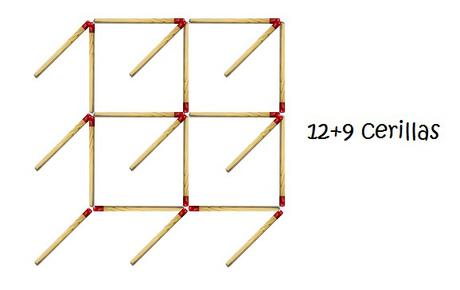
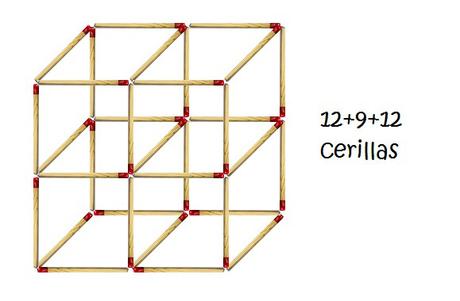
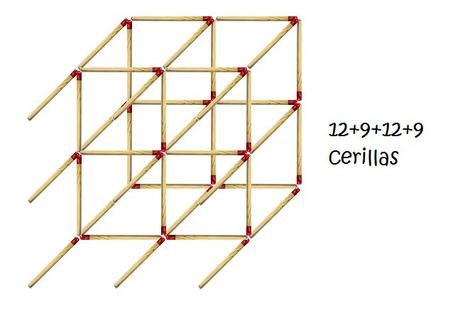
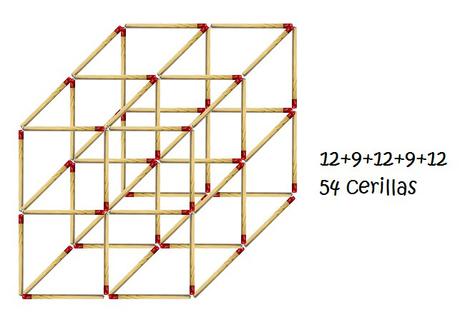
Mi intuición me dice que sí porque hay muchas cerillas comunes, pero vamos a comprobarlo.

Para que no se nos haga muy tedioso esto de contar los cuadrados, vamos a buscarnos un sistema que lo haga más sencillo.

Por cada “malla” o configuración de lado 2 cerillas como la que nos ha servido de punto de partida tenemos

5 cuadrados.

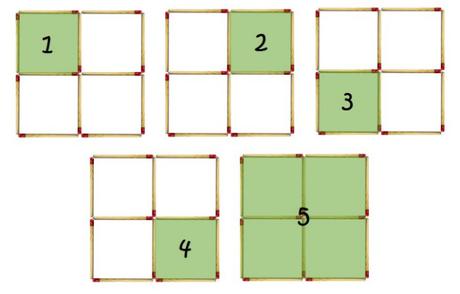
Así que basta con ver cuantas “mallas” o configuraciones así tenemos en nuestro cubo de cerillas

Tenemos 9 “mallas” con esa configuración y, como cada una tiene 5 cuadrados, hemos conseguido un total de…

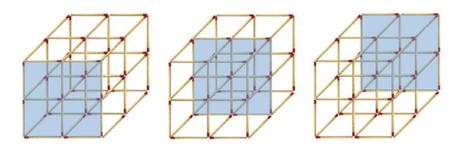
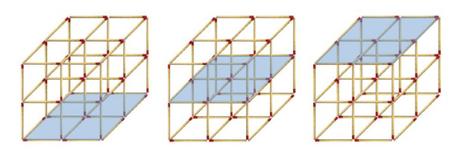
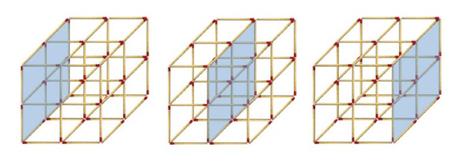
¡¡¡45 cuadrados!!!

Pues sí, hemos conseguido dos cuadrados más que de la otra manera.

Lo cierto es que a veces nos limitamos nosotros mismos y, en muchas ocasiones, basta con mirar las cosas desde otra perspectiva para llegar a mejores soluciones.

Muchas gracias por vuestro tiempo y espero de verdad que os haya gustado.

Tanto las imágenes utilizadas como el problema propuesto y resuelto son de autoría propia.