SOLUCIÓN ¿Cuántos hexágonos hay dibujados en la imagen?

El problema que planteé decía así:

“¿Cuántos hexágonos puedes dibujar siguiendo las líneas blancas del dibujo de la siguiente imagen?”

Veamos la SOLUCIÓN, o quizás debiera decir la solución que os propongo:

Lo primero por lo que podemos empezar es buscando hexágonos regulares, es decir, que tengan los 6 lados y los 6 ángulos iguales (para ser más exactos deberíamos decir congruentes entre sí) que son los que la mayor parte de la gente tiene en mente cuando se le habla de hexágonos y, además, la forma de la figura invita a ello:

 

 Pero no todo es regular, así que vamos a buscar ahora hexágonos irregulares:

 
 
 
 
 
 
 
 
 

 Este “dibujo” parece que ya no nos da para más, así que vamos a seguir buscando más hexágonos irregulares con otra forma:

 
 
 
 
 
 

 Seguimos buscando…

 
 
 
 
 
 

 ¡Ya llevamos 44 hexágonos!

Pero… ¿esos son todos los que hay?

Quien me conozca ya un poco sabrá que la respuesta es NO.

Hasta ahora, todos los hexágonos que hemos identificado, regulares e irregulares, eran polígonos simples.

Polígonos simples (en nuestro caso hexágonos simples) son los que, muy a mi pesar, vemos casi siempre dibujados en cualquier libro de texto de matemáticas cuando se habla de polígonos y, consecuentemente, se suele tener en mente.

En un polígono simple ningún par de lados no consecutivos se corta (no es el caso de los lados consecutivos, que se cortan en el vértice).

Pero, puede ocurrir que uno o más pares de lados no consecutivos se corten, y en ese caso lo que tenemos son polígonos complejos.

Sí… también hay polígonos complejos, que no todo es simple en esta vida, de hecho casi nada lo es… o según cómo se mire.

Un ejemplo de hexágono complejo podría ser el siguiente:

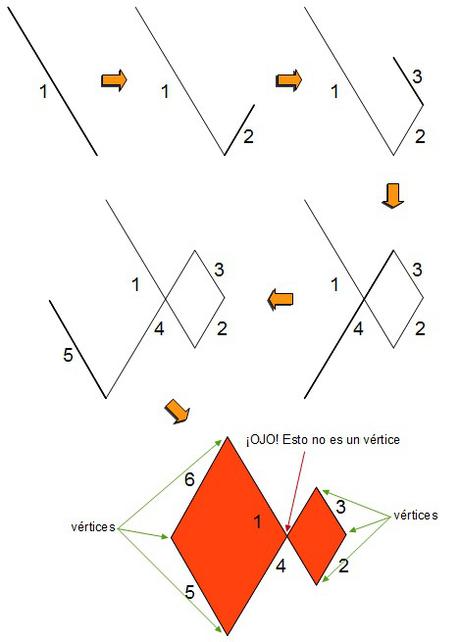
Como se indica en la última figura, donde ya está el hexágono complejo dibujado en su totalidad, el punto donde se cortan los lados 1 y 4 no es un vértice, pues por definición un vértice es el punto de intersección de dos lados consecutivos, y éstos no lo son.

Ahora sabiendo esto, volvamos a nuestro problema y sigamos buscando hexágonos, pues con los hexágonos complejos se nos abre ahora todo un “mundo de posibilidades”…

Podemos buscar, por ejemplo, hexágonos complejos del estilo de éste que hemos visto…

 
 
 
 
 
 

o estos otros…

 
 
 
 
 
 
 
 

 … y estos hexágonos también…

 
 
 
 
 
 

y podemos seguir así, porque es cuestión de ir cambiando tamaños y posiciones…

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

… o estos otros, parecidos a los anteriores…

 
 
 
 
 
 

 ¡132 hexágonos!

¿Hay alguno más?

Yo, personalmente, no he encontrado ninguno más, pero no descarto que se me haya “escapado” alguno pues, siendo sincero, cuando dibujé la figura del problema para proponerlo y me puse a buscar hexágonos, hasta yo mismo me sorprendí del número de hexágonos que obtuve.

Así que, si encontráis algún hexágono más os invito a que me lo comentéis, ya que este blog lo hacemos entre todos.

Tenía ganas de proponer un problema así para poder tratar los polígonos complejos, porque por culpa de las representaciones que se suelen emplear en los libros de texto, parece que los hexágonos sólo sean regulares y, aun cuando se sobrepasa esta barrera y se aceptan también los irregulares, da la sensación de que sean “más hexágonos” los convexos que los no convexos; Y ya no digamos los hexágonos complejos que, por tener la “mala suerte” de ser polígonos complejos, parece que ni sean hexágonos. Y es que, si bien en algunos libros se mencionan los polígonos complejos cuando se trata la clasificación de los polígonos, diferenciándolos del universo de los simples, después se convierten en una especie en peligro de extinción en los ejercicios y problemas, quedando como una mera anécdota.

Así es que, a todas aquellas personas que no hayan llegado a ver tantos hexágonos en la imagen que propuse, yo les diría que no es culpa suya, sino más bien de cómo se suelen enseñar las cosas.

Espero no haberos aburrido y ojalá este problema que decidí proponer le haya servido a alguien para saber algo más sobre los polígonos y ampliar un poco su concepto de polígono y, en concreto, de hexágono, o simplemente para haber pasado un rato entretenido.

---

¿Te ha gustado?

Este blog se presenta a los Premios Bitácoras 2015 en la categoría de Educación y Ciencia.

Si consideras que merece tu VOTO, puedes dárselo pinchando en la IMAGEN que te muestro a continuación.

BREVES INSTRUCCIONES PARA VOTAR:

Tan solo hay que pinchar en el enlace de la imagen y validarse con una cuenta de Facebook o Twitter (lo hacen para que una persona no pueda votar varias veces al mismo blog) y después en la pantalla que sale, bajar hasta el final y pinchar en el botón que dice “votar”.

¡Muchísimas gracias por estar ahí!