El acertijo propuesto es el siguiente:
¿Qué ficha debería ser la última?
Se trata de encontrar el razonamiento que se ha seguido para obtener cada una de las fichas de dominó en el orden en que aparecen y, conocido éste, poder deducir cuál es la ficha del final que está girada.
La regla lógica que se utilice tiene que ser la misma para todas las fichas (excepto la primera, que es el punto de partida y viene fijada).
¿Lo has intentado ya?
¿Qué ficha crees que es?
Si estás intentándolo o no lo has hecho aún, no sigas leyendo y piénsalo.
Si ya lo has hecho y quieres comprobar la solución… sigue leyendo.
Vamos con ello…
Tendemos a buscar soluciones complicadas, tanto más cuanto más conocimientos se tienen en matemáticas, sin embargo en este caso eso nos puede traicionar, porque la solución es más sencilla de lo que parece.
La clave está en ver las fichas de dominó como fracciones. La línea horizontal situada en la parte central de la ficha es la línea divisoria que separa el numerador y el denominador de la fracción.
Así, la primera ficha es…
Vuelve a mirar ahora la secuencia de fichas sabiendo que representan fracciones…
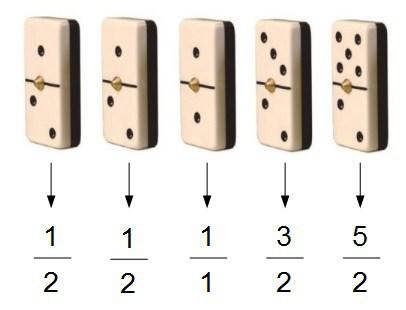
¿Ves ahora cómo se obtienen?
Si sigues sin verlo, puede que te ayude bastante sustituir la tercera fracción por una fracción equivalente con denominador 2 (que es el que tienen el resto de las fracciones)…
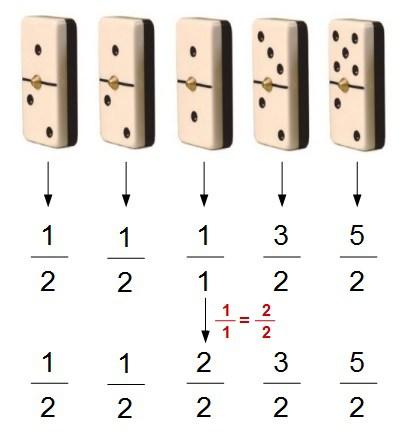
¿Mejor ahora?
¡Exacto!
Cada fracción (excepto la primera que está fijada) se obtiene como suma de las dos anteriores. Traducido en fichas es que cada ficha (salvo la primera) se obtiene como suma de las dos anteriores.
Lo vemos. La segunda ficha se obtiene de…
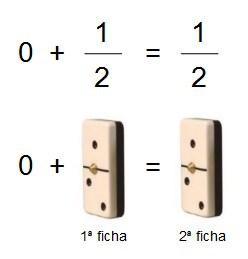
La tercera ficha…
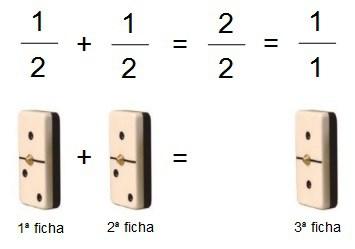
… cuarta ficha…
… quinta ficha…
Y, la última ficha (la que estaba girada) es…
Con lo que la secuencia de fichas de dominó completa queda:
En resumen, sería algo así como una serie de fracciones “a lo Fibonacci” (cada término se obtiene como suma de los dos anteriores) o, ya que se trata de fichas de dominó, un dominó “a lo Fibonacci”.
Por cierto, creo que es un recurso a modo de juego interesante para cuando se empieza a trabajar en clase la suma de fracciones y la reducción de fracciones con fracciones equivalentes.
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure