Sumando voy sumando vengo

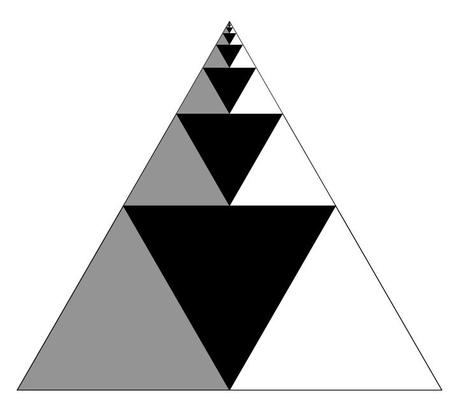
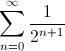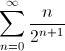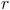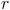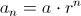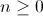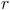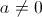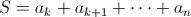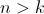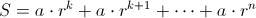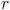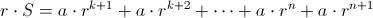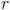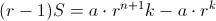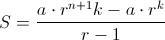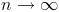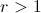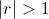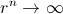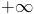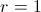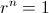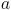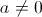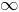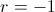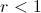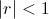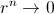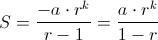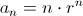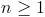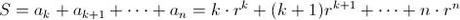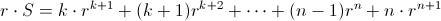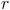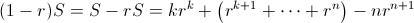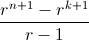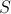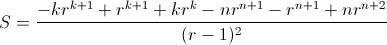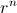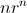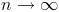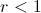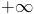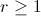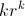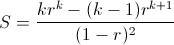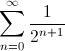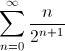Imagen extraída de Wikipedia

Os voy a plantear un reto (extraído de Spiked Math). Si te dan a elegir entre 1 Euro, Euros ó Euros... ¿qué elegirías? Antes de responder, quizás te convenga seguir leyendo este post, ya que en él vamos a sumar.
Sumar muchos números suele ser tarea difícil... y si encima tenemos infinitos de ellos... ya la cosa se complica. Sin embargo, hay sumas finitas e infinitas que son sencillas de calcular y que suelen aparecer, además con frecuencia. Hace ya tiempo que vimos en este mismo blog cómo sumar uno de esos tipos de series, las series telescópicas. Te animo a que leas esa entrada también.
Hoy nos vamos a centrar en otros dos tipos de series muy conocidas: las geométricas y las aritmético-geométricas. Y para hacer las cosas sencillas, vamos a sumar desde una cantidad finita de términos consecutivos hasta la serie completa.
Comencemos con las primeras. ¿Qué es una progresión geométrica? Fácil, aquélla en la que el cociente entre dos términos consecutivos siempre es el mismo: . O dicho de otro modo, una progresión geométrica es la que cada término se consigue a partir del anterior, multiplicándolo por una constante . El término general será para cada , donde recibe el nombre de razón de la progresión geométrica y es el valor inicial.
Bien, ahora vamos a sumar una cantidad finita de términos consecutivos. Llamemos donde ; de esta forma, . Si multiplicamos por , tendremos que y ahora sólo queda restar los términos que tengan la misma potencia de para obtener que , de donde , lo que nos da la fórmula que se enseña de memoria: el último elemento por la razón menos el primero dividido entre la razón menos 1.
¿Y qué pasa si sumamos hasta el infinito? Pues que sólo hay que conseguir que en la fórmula anterior. Y aquí la cosa depende. Vamos a centrarnos en los casos en que la razón de la serie es positiva. Si (en realidad es cierto si ) entonces y tendríamos que la suma de los infinitos términos divergería a ; si , entonces y nuestra progresión aritmética sería constante igual a , por lo que la suma de infinitos daría otra vez (por cierto, el caso nos da un caso extraño que ni converge ni diverge); finalmente, si (válido también si ) se tiene que de donde la suma de los infinitos términos será , es decir, el primer término dividido entre 1 menos la razón, que es la fórmula que se enseña.
Pasemos ahora al segundo tipo de progresiones, las aritmético-geométricas. Se trata de una mezcla entre las geométricas y las aritmáticas... bueno, mejor veamos su término general: con .Para sumarla vamos a utilizar el mismo truco anterior. Llamamos , entonces . Si ahora restamos los términos con las mismas potencias de , llegamos a que . Y resulta que lo que tenemos entre paréntesis es la suma de términos consecutivos de una progresión geométrica, que ya sabemos lo que vale: . Ahora basta despejar y obtener que .
Si pretendemos ver qué ocurre si sumamos infinitos términos de una sucesión aritmético geométrica, sólo hay que tener en cuenta que y se comportan igual cuando , es decir, convergen a 0 si y divergen a si . Por lo tanto, la suma de infinitos términos de una sucesión aritmético-geométrica que comienza en es .
Volvamos al problema del principio: ¿qué elegirías? ¿1 Euro, Euros ó Euros? Ahora ya tienes las herramientas para responder. Pero procura no utilizar las fórmulas, sino aplicar el método para obtenerlas, para resolver este acertijo.
Suerte.
Tito Eliatron Dixit 
 
Si te ha gustado esta entrada, puedes dejar un comentario directamente en Tito Eliatron Dixit.