Tener la razón (II): Todos seremos gordos

El cómico Eugene Mirman cuenta el siguiente chiste sobre las estadísticas. Dice que a la gente le dice, “He leido que el 100% de los americanos son asiáticos”. ¡Pero hombre!, dicen sus compañeros confundidos, ¡TÚ NO ERES ASÍATICO!, lo cual provoca el remate del chiste: “Pero yo leí que lo soy!” Pensé exáctamente en esa frase cuando hace un tiempo atrás me encontré con un artículo sobre la obesidad en EEUU. El título tenía la siguiente pregunta desconcertante: “¿Todos los americanos serán obesos o tendrán sobrepeso?” No satisfechos con la pregunta, nos dan hasta una respuesta. ¡Sí! Para el año 2048. ¿No me lo creen? Aquí tenéis el estudio.

El estudio provocó mucha material para la prensa…siempre tan dada a las mentiras y el sensacionalismo. La cadena estadounidense ABC advirtió que se avecinaba una “apocalípsis” de obesidad. Otros titulares decían “Nos estamos poniendo más gordos” o alguna variante. Los resultados del estudio resonaron con esa famosa ansiedad moral tan característica de los estadounidenses cuando piensan en su “estatus” moral como país y a nivel personal. En los 50 y 60 se decía que los varones empezaban a tener pelo largo y en consecuencia “los comunistas” iban a darle una paliza a EEUU…cuando es justamente hoy en día el hecho de que probablemente los más izquierdistas o en todo caso anarquistas son los que llevan melena larga. En los años 80 se decía que los niños jugaban demasiado en el salón de juegos y que por eso los japoneses o chinos nos iban a comer vivos. El caso es que todas las épocas han sufrido de algún tipo de “pánico moral” por esta u otra razón(es). Ahora el pánico es la obesidad. Vamos a morir todos rodeados de bloques enteros de grasa y sin poder movernos por la gordura, tendremos todos microchips del estado, etc, etc. Ya conocéis las conspiranoias.

En fin, tengo buenas notícias. NO TODOS vamos a sufrir de obesidad para el año 2048. ¿Por qué? Por lo que dije en la entrada anterior cuando critiqué el razonamiento de la mayoría de gente conservadora. Porque NO TODAS LAS CURVAS SON RECTAS. Pero todas las curvas, como ya nos advirtió el bueno de Newton, son muy muy parecidas a una recta. Precisamente ese concepto es lo que está detrás del famoso concepto en estadísticas matemáticas llamado Regresión lineal. Para las ciencias sociales, para el análisis de datos, esta herramienta es tan útil como el destornillador en una casa. Tarde o temprano por supuesto que lo vas a utilizar o vas a leer algún estudio fruto de la regresión lineal. Cada vez que lees que gente con más primos son más felices, o que los países con más restaurantes de comida rápida son más liberales, etc, etc, todos estos “estudios” son frutos de la regresión lineal.

Funciona de la siguiente manera:

Quieres relacionar dos cosas. Pongo un ejemplo: El coste anual de una universidad y los resultados en las pruebas famosas aquí en EEUU conocidas como el SAT (un examen que yo imparto para mis alumnos en formación). El pensamiento corriente dirá que cuanto más alto el resultado del alumno en el SAT, más cara la universidad. Dicho de otra forma: las universidades con los alumnos que más altos resultados consiguieron en el SAT son las más caras. Sin embargo, la muestra de datos nos demuestra que esa observación no es ninguna ley universal. Hay ejemplos de universidades bastante caras en las que los resultados del SAT no son nada impresionantes, mientras que hay otras universidades baratas (y sí, privadas…y ojo, digo “baratas” PARA LOS ESTÁNDARES americanos, no para un español que está acostumbrado a que casi todas las universidades sean públicas). Os doy un ejemplo de una universidad relativamente barata donde el SAT es bastante alto — la famosa universidad ultraconservadora y cristiana protestante, Patrick Henry College. El coste de esta universidad asciende a $27.922 anuales…¡baratísimo si comparamos con otras universidades privadas! No obstante, es verdad que si analizas las universidades más caras de EEUU, ciertamente se puede observar algunas tendencias. Aquí va una gráfica con los datos. La siguiente gráfica demuestra, claro, que las universidades más caras también suelen tener los resultados del SAT más elevados. Pero ¿por cuanto MÁS? Ahí es donde el análisis de regresión lineal es clave.

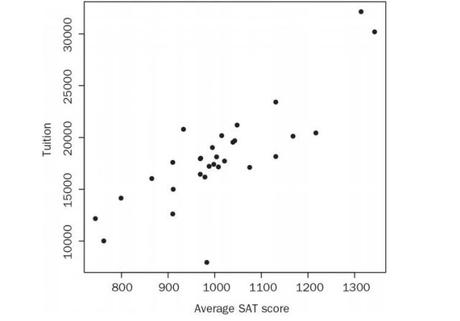
Aplicando el análisis de regresión lineal, mirad la siguiente gráfica ajustada:

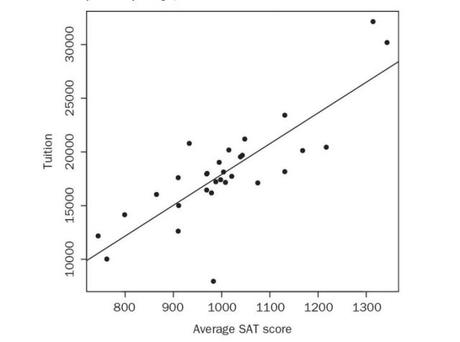
El valor de la pendiente de la recta que vemos en la gráfica es aproximadamente 28. ¿Qué significa eso? Si la matrícula anual fuese realmente el resultado de la puntuación en el SAT, cada punto adicional en el SAT correspondería con $28 dólares más por cada punto adicional. Si todos los alumnos del primer curso consiguieran aumentar 50 puntos en el SAT, se les podría cobrar $1.400 más anuales (ó, desde el punto de vista de los padres, si tu hijo consigue mejorar 100 puntos más te costará $2.800 dólares de más. ¡Vale más que un niño bobo!

La regresión lineal es una excelente herramienta. Es versátil, escalable, y tremendamente fácil de ejecutar si tienes Excel y unos datos. Funciona tanto para dos variables como el ejemplo que os he dado como para miles de variables. Esto es una ventaja, pero también puede ser una debilidad. He dicho que esta herramienta es como un destornillador, y eso es verdad; pero en otro sentido, es más bien como un serrucho. Si la utilizas sin prestar atención, los resultados pueden ser espantosos. Mucho cuidado con hacer extrapolaciones lineales descuidadamente. El mejor ejemplo que conozco sobre esta equivocación la escribió no un estadístico ni un matemático (sí, claro que distingo entre matemáticos y estadísticos). No, ninguno de los dos. Fue Mark Twain, en su obra sobre la vida en el Misisipí escribió el mejor ejemplo que conozco sobre la extrapolación lineal equivocada. Si podéis entender la lectura en inglés, aquí va el extracto de su excelente texto.

Entonces volvemos a la pregunta inicial. ¿Qué porcentaje de estadounidenses serán gordos en el 2048? No cabe duda que en las últimas décadas, hay muchísimas más personas gordas. Solo os basta con ver cualquier foto de una ciudad en USA en los años 50 y 60 y, muy al contrario de hoy en día, en aquellos tiempos el estereotipo del americano era el siguiente: hombre/mujer rubia, altos, DELGADOS. Las muñecas “Barbie” imitaban ese ideal y ese estereotipo. Incluso en aquellos tiempos el estereotipo de mujer gorda lo tenía la mujer mediterránea. Cada vez que salía una mujer española, italiana o griega en alguna película anglosajona, la ponían vestida toda de negro (si era mayor) y algo gordita (y velluda). Razón no les faltaba…porque en esos años España, por ejemplo, estaba MUYYYY lejos de eso de la “dieta mediterránea”, otro mito más de nuestros tiempos. España nunca fue un país 100% mediterráneo y se comía muchas alubia, potajes, chorizos y otros productos cárnicos de casquería y demás que hoy en día los “finolis” de la dieta mediterránea ni conocen. ¿Aceite de oliva? Más bien manteca y aceite de girasol en los años 70.

A principios de los 70, el porcentaje de americanos con sobrepeso no alcanzaba ni el 50%. Entrando la década de los 90, ya ascendía a casi el 60% y en el 2008, casi el 75% de los estadounidenses eran gordos. Si utilizamos estos datos y hacemos otro análisis de regresión lineal, veríamos que para el año 2048, la recta pasaría el 100%. Por eso Wang en su “estudio” afirmó que TODOS los americanos serían gordos en el 2048 SI CONTINÚAN LAS TENDENCIAS ACTUALES.

Pero he ahi el error. Las “tendencias actuales” NO son eternas ni permanentes. NO PUEDE SER ASÍ. De ser así, para el año 2060, tendríamos una cifra gigantesca — el 109% de los americanos serían gordos. Imposible. En realidad, la gráfica se acerca al 100%, así:

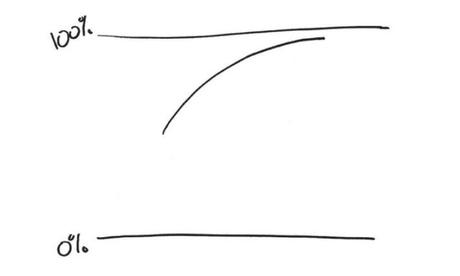
La gordura es como el coronavirus actual — la cifra sigue aumentando y aumentando hasta que, INEVITABLEMENTE, tiene que bajar. De hecho, ya los datos demuestran que los americanos empiezan a estabilizar en su sobrepeso y la cifra se va manteniendo e incluso bajando, después de alcanzar su pico hace unos años.

Pero el estudio que enlacé al principio sobre la obesidad esconde otro crimen PEOR contra las matemáticas y el sentido común. Hacer un análisis de regresión lineal es fácil. Una vez has hecho uno, el resto ya lo puedes hacer casi con los ojos cerrados. Así pues, Wang y sus colegas dividieron los datos por raza y sexo. Los varones de raza negra, por ejemplo, eran menos propensos a ser gordos que el resto de americanos y más importante aún, su índice de sobrepeso crecía solo a la mitad en comparación con los demás. Si superponemos la proporción de varones negros gordos sobre la proporción de americanos con sobrepeso en su conjunto, junto con las regresiones lineales de Wang y sus colegas, veríamos que no sería hasta el año 2095 en el que TODOS ellos serían gordos. En el año 2048, “solo” el 80% será gordo. ¡¡¡MUY BIEN, SEÑORES NEGROS!!!

¿No veis el problema? Si “TODOS” los americanos serán gordos en el 2048, ¿dónde estarán esos uno de cada cinco varones negros sin sobrepeso? ¿En otro planeta, quizá? Esa contradicción tan básica no se menciona en el “estudio”. Es el equivalente epidemiológico de afirmar que hay -4 gramos de agua que quedan en el cubo. NO TIENE MÉRITO ALGUNO.

Las matemáticas son la ciencia de NO EQUIVOCARSE sobre las cosas. Sin la estructura rigurosa de las matemáticas, no te vale el “sentido común”. Las matemáticas te permiten dudar, pero dudar con principios. Una de las grandes ventajas de las matemáticas es precisamente nuestra capacidad de dudar todo lo que se nos dice salvo que se demuestre sin lugar a dudas con el rigor de la lógica. Si no quieres equivocarte, DEBES SABER LO QUE NO SABES.