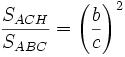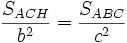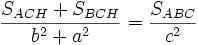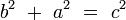“En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”. Esta sencilla definición que casi todos conocemos puede que se haya olvidado. Pues bien, os dejo el teorema y sus múltiples demostraciones para aquellos que la necesiten para su aprendizaje, para recordaros esta maravilla de las matemáticas o simplemente con el fin de que aprendáis algo que no sabíais.
a2 + b2 = c2
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
Teorema de Pitágoras generalizado
Si en vez de construir un cuadrado, sobre cada uno de los lados de un triángulo rectángulo, construimos otra figura, ¿seguirá siendo cierto, que el área de la figura construida sobre la hipotenusa es igual a la suma de las áreas de las figuras semejantes construidas sobre los catetos?
(Debajo de los dibujos siguientes se accede a la comprobación numérica en las figuras que se representan)



Teorema de Pitágoras con polígonos regulares

Teorema de Pitágoras con semicircunferencias
Teorema de Pitágoras con polígonos irregulares
Aunque sin demostración, podemos concluir que dado un triángulo rectángulo, si construimos figuras semejantes sobre cada uno de sus lados, se verifica que el área de la figura construida sobre la hipotenusa es igual a la suma de las áreas de las figuras construidas sobre los catetos.
_________________________________________________________________________________________________________________________________________
DEMOSTRACIONES DEL TEOREMA DE PITÁGORAS
-
Demostracion de Pitágoras
Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales.[1]
Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente.
Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.
- De la semejanza entre ABC y AHC:
y dos triangulos son semejantes si hay dos o más ángulos congruentes.
- De la semejanza entre ABC y BHC:
Los resultados obtenidos son el teorema del cateto. Sumando:
Pero  , por lo que finalmente resulta:
, por lo que finalmente resulta:
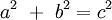
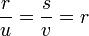
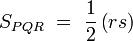
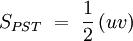
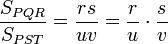
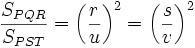
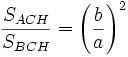
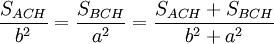 (I)
(I)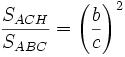
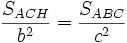
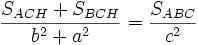
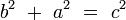
Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.
Los triángulos PQR y PST son semejantes, de manera que:
siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:
obtenemos después de simplificar que:
pero siendo  la razón de semejanza, está claro que:
la razón de semejanza, está claro que:
Es decir, “la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza”.
Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:
que de acuerdo con las propiedades de las proporciones nos da:
y por la semejanza entre los triángulos ACH y ABC resulta que:
pero según (I)  , así que:
, así que:
y por lo tanto:
quedando demostrado el teorema de Pitágoras.
-
Demostración de Platón: Menón
Esta filosófica pregunta forma parte del Menón de Platón, y a su tenor no parece que la Geometría vaya a hacer acto de presencia en el Diálogo, pero el filósofo es quien maneja los hilos y unas páginas más adelante nos encontramos con cuadrados y superficies. En ese fragmento, Platón habla de que conocer es recordar. Cuando creemos estar aprendiendo, lo que sucede en realidad es que recordamos las verdades que nuestra alma pudo percibir de forma inmediata antes de encarnarse en el cuerpo.
En el texto Sócrates se lo demuestra a Menón llamando a uno de sus esclavos, que nunca ha sido educado, pero que, sin embargo, es capaz de llegar a demostrar el teorema de Pitágoras. Sócrates le plantea el problema de la duplicación del cuadrado. Sucesivas preguntas van sacando de la mente del esclavo la solución del problema, con lo que pretendidamente aquél no hizo sino “recordar” lo que ya “sabía”. Ese método para sacar esos conocimientos es la mayéutica, en la cual, el individuo que conduce al otro hacia el conocimiento, como en este caso hace Sócrates, desempeña una función similar a la de una partera, donde lo que logra extraer de su interlocutor, es el conocimiento de lo verdadero.
Platón construye un cuadrado cuyo lado es de dos unidades (izquierda, gris). Su área vale lo de cuatro unidades cuadradas. Trazando un nuevo cuadrado sobre su diagonal AB, obtiene un cuadrado de ocho unidades cuadradas (centro, azul), doble superficie de la del primero. Hasta aquí la duplicación del cuadrado. Pero también se ha demostrado el teorema de Pitágoras (derecha): el área del cuadrado azul (8u2) construido sobre la hipotenusa AB del triángulo rectángulo ABC, es igual a la suma de las áreas de los cuadrados grises (4u2 cada uno) construidos sobre los catetos AC y BC. Generalizando: cada uno de los cuadrados construidos sobre la hipotenusa (la diagonal del cuadrado inicial) contiene cuatro de dichos triángulos.
Queda demostrado el teorema de Pitágoras, si bien restringido a los triángulos rectángulos isósceles.
- Demostración de Euclides: proposición I.47 de Los Elementos
El descubrimiento de los números irracionales por Pitágoras y los Pitagóricos supuso un contratiempo muy serio.[3] De pronto, las proporciones dejaron de tener validez universal, no siempre podían aplicarse. La demostración de Pitágoras de su teorema se basaba muy probablemente en proporciones, y una proporción es un número racional. ¿Sería realmente válida como demostración? Ante esto, Euclides elabora una demostración nueva que elude la posibilidad de encontrarse con números irracionales.
El eje de su demostración es la proposición I.47 de Los Elementos:
- Si un paralelogramo y un triángulo tienen la misma base, y están comprendidos entre las mismas paralelas, entonces el área del paralelogramo es doble de la del triángulo. Esto es tanto como decir que a igual base y altura, el área de aquél dobla a la de éste.
Tenemos el triángulo ABC, rectángulo en C, y construimos los cuadrados correspondientes a catetos e hipotenusa. La altura CH se prolonga hasta J. Seguidamente se trazan cuatro triángulos, iguales dos a dos:
- Triángulos ACK y ABD: son iguales, pues siendo AD=AC, y AK=AB, necesariamente BD=CK. Sus tres lados son iguales.
- Triángulos ABG y CBI: análogamente, AB=BI, y BG=BC, así que AG=CI. Sus tres lados son asimismo iguales.
Abundando en las anteriores consideraciones, nótese que un giro con centro en A, y sentido positivo, transforma ACK en ABD. Y un giro con centro en B, y sentido también positivo, transforma ABG en CBI. En la demostración de Leonardo da Vinci nos encontraremos de nuevo con giros que demuestran la igualdad de figuras.
Veamos seguidamente que:
- Las paralelas r y s comprenden al triángulo ACK y el rectángulo AHJK, los cuales tienen la misma base, AK. Por tanto de acuerdo con la proposición I.47 AHJK tiene doble área que ACK.
- Las paralelas m y n contienen a ABD y ADEC, cuya base común es AD. Así que el área de ADEC es doble de la de ABD.
Pero siendo ACK=ABD, resulta que el rectángulo AHJK y el cuadrado ADEC tienen áreas equivalentes. Haciendo razonamientos similares con los triángulos ABG y CBI, respecto al cuadrado BCFG y al rectángulo HBIJ respectivamente, concluimos que éstos últimos tienen áreas asimismo iguales. A partir de aquí, es inmediato que la suma de las áreas de los cuadrados construidos sobre los catetos, es igual al área del cuadrado construido sobre la hipotenusa.
-
Demostración de Pappus
Unos 625 años después que Euclides, Pappus parece seguir su senda, y desarrolla una demostración del teorema de Pitágoras basada en Elementos I.36:
- Dos paralelogramos de igual base, y entre las mismas paralelas, tienen superficies equivalentes.
Partimos del triángulo ABC rectángulo en C, sobre cuyos catetos e hipotenusa hemos construido los cuadrados correspondientes.
Prolongando CH hacia arriba se obtiene el rectángulo CEGI cuya diagonal CG determina en aquél dos triángulos rectángulos iguales al triángulo ABC dado:
- Los ángulos agudos GCI y ABC tienen sus lados perpendiculares
- El lado CI es igual al lado CB
En consecuencia los triángulos rectángulos ABC, ICG y EGC tienen sus tres lados iguales.
- Los paralelogramos ACGF y AHMN tienen la misma base CG=HM, y están comprendidos entre las mismas paralelas, r y s. Por lo tanto tienen la misma superficie (Elementos I.36)
- Aplicando el mismo principio a ACGF y ACED –base común AC, y paralelas m y n- resulta que ambos paralelogramos tienen superficies asimismo equivalentes.
De 1) y 2) se sigue que las superficies de ACED y AHMN son iguales.
Análogamente:
- CGJB y BLMH tienen la misma base CG=MH, y están comprendidos entre las paralelas s y t. Sus superficies son equivalentes.
- CGJB y CIKB tienen base común CB, y están entre las paralelas o y p. Sus superficies son iguales.
De dónde se deduce la equivalencia de las superficies de BLMH y de CIKB.
El teorema de Pitágoras queda demostrado.
-
Demostración de Bhaskara
Bhaskara II, el matemático y astrónomo hindú del siglo XII, nos da la siguiente demostración del teorema de Pitágoras.
Con cuatro triángulos rectángulos de lados a, b y c se construye el cuadrado de lado c –izquierda-, en cuyo centro se forma otro cuadrado de lado (a-b).
Redistribuyendo los cuatro triángulos y el cuadrado de lado (a-b), construimos la figura de la derecha, cuya superficie resulta ser la suma de la de dos cuadrados: uno de lado a –azul- y otro de lado b -naranja-.
Se ha demostrado gráficamente que c2 = a2 + b2
Algebraicamente: el área del cuadrado de lado c es la correspondiente a los cuatro triángulos, más el área del cuadrado central de lado (a-b), es decir:
expresión que desarrollada y simplificada nos da el resultado c2 = a2 + b2, y el teorema queda demostrado.
-
Demostración de Leonardo da Vinci
En el elenco de inteligencias que abordaron el teorema de Pitágoras no falta el genio del Renacimiento, Leonardo da Vinci. Su demostración es una de las más hermosas.
Partiendo del triángulo rectángulo ABC con los cuadrados de catetos e hipotenusa, Leonardo añade los triángulos ECF y HIJ, iguales al dado, resultando dos polígonos, cuyas superficies va a demostrar que son equivalentes:
- Polígono ADEFGB: la línea DG lo divide en dos mitades idénticas, ADGB y DEFG.
- Polígono ACBHIJ: la línea CI determina CBHI y CIJA.
Comparemos los polígonos destacados en gris, ADGB y CIJA:
- De inmediato vemos que tienen tres lados iguales: AD=AC, AB=AJ, BG=BC=IJ
- Asimismo es inmediata la igualdad entre los ángulos de los siguientes vértices:
- A de ADGB y A de CIJA
- B de ADGB y J de CIJA
Se concluye que ADGB y CIJA son iguales.
De modo análogo se comprueba la igualdad entre ADGB y CBHI.
Además, de un modo semejante a lo explicado en la demostración de Euclides, nótese que un giro de centro A, y sentido positivo, transforma CIJA en ADGB. Mientras que un giro de centro B, y sentido negativo, transforma CBHI en ADGB.
Todo ello nos lleva a que los polígonos ADEFGB y ACBHIJ tienen áreas equivalentes. Pues bien, si a cada uno le quitamos sus dos triángulos –iguales- las superficies que restan forzosamente serán iguales. Y esas superficies no son sino los dos cuadrados de los catetos en el polígono ADEFGB, por una parte, y el cuadrado de la hipotenusa en el polígono ACBHIJ, por la otra. El teorema de Pitágoras queda demostrado.
-
Demostración de Garfield
James Abram Garfield (1831-1881), el vigésimo Presidente de los Estados Unidos [5] , desarrolló una demostración del teorema de Pitágoras publicada en el New England Journal of Education.
Garfield construye un trapecio de bases a y b, y altura (a+b), a partir del triángulo rectángulo de lados a, b y c. Dicho trapecio resulta compuesto por tres triángulos rectángulos: dos iguales al dado, y un tercero, isósceles de catetos c. En consecuencia:
como corresponde a la superficie del trapecio, pero asimismo tenemos una figura compuesta por tres triángulos, dos de ellos iguales, de modo que:
igualando:
lo que finalmente nos da c2 = a2 + b2, y el teorema está demostrado.
a
a
a
Fuente: http://es.wikipedia.org/













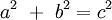
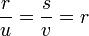
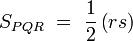
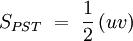
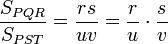
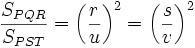
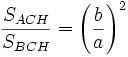
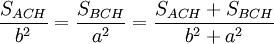 (I)
(I)