Teoría de grupos y virus

Las matemáticas, incluso más abstractas, permiten aplicaciones directas a numerosos campos, entre ellos la Biología y la Medicina. Se ha visto en esta pandemia de la Covid-19 la utilidad de los modelos epidemiológicos (SIR y derivados, cadenas de Markov, series temporales) basados en las ecuaciones diferenciales, la Estadística y los procesos estocásticos, pero no son los únicos.

Reidun Twarock

En esta entrada vamos a describir el trabajo realizado por la investigadora Reidun Twarock, nacida en Alemania pero que trabaja como bióloga matemática en la Universidad de York. Su trabajo trata de responder a la dificultad para encontrar remedios para las enfermedades que provocan. Este problema viene de la enorme capacidad de los virus para mutar, cambiando las estructuras que se usan para diseñar las drogas que los ataquen. El trabajo de Twarock y su equipo ha servido para conocer mejor esas estructuras, determinar sus limitaciones y conocer cómo se forman los virus, cómo evolucionan y cómo infectan a los organismos vivos que los albergan.

Como comentaba la propia Twarock en una reciente entrevista en 2019: “Mi trabajo sobre la estructura de los virus ha permitido una profunda comprensión de los ciclos de vida virales que sólo se podría lograr a través de la lente de la geometría viral. Un resultado muy emocionante es el descubrimiento del código de ensamblaje de los virus que ha anulado el paradigma existente en el ensamblaje de los virus y ha abierto nuevas vías para la intervención antiviral.”

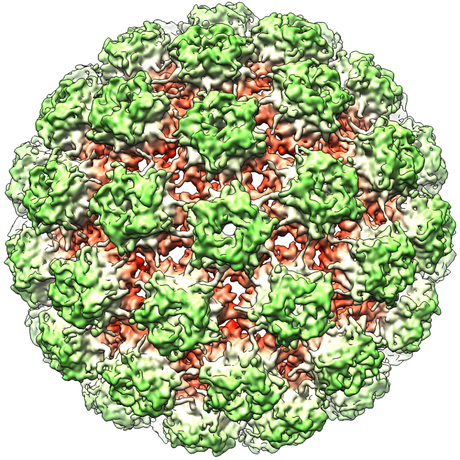
Papillomavirus

En esa misma entrevista, cuenta cómo comenzó a interesarse por los virus: “En una conferencia de Física Matemática en París en 2002, asistí a una charla sobre virus icosaédricos por el biofísico Robijn Bruinsma de la UCLA. Como la simetría icosaédrica no es cristalográfica, me di cuenta de que las técnicas matemáticas en las que estaba trabajando en ese momento podrían desarrollarse aún más para aplicaciones en virología. Sin embargo, yo estaba demasiado involucrada con otros proyectos para actuar inmediatamente sobre esta observación. Trabajando con el matemático Walter Mazorchuk en la Universidad de Uppsala el verano siguiente, tuve la oportunidad de visitar al virólogo Lars Liljas en el Biomedicum. Llamó mi atención sobre el rompecabezas estructural de los virus cancerígenos que luego abordé en los próximos meses con mi formación en simetrías no cristalográficas y mosaicos aperiódicos. Este fue el comienzo de la Virología Matemática.”

Lo que sigue es un resumen de los principales resultados matemáticos y sus consecuencias para nuestra comprensión de los virus y la terapia antiviral, resumen recogido desde su artículo “Viruses and Geometry: Group, Graph and Tiling Theory Open Up Novel Avenues for Anti-Viral Therapy”, publicado en London Mathematical Society Impact150 Stories 1 (2016) 63-68. En concreto, el interés de Twarock está en el estudio de

1. Extensiones afines de grupos de Coxeter no cristalográficos y geometría del virus.

2. Teoría del mosaico viral en virología y bio-nanotecnología.

3. Cómo las transiciones de retículos proporcionan información sobre transiciones estructurales importantes para la infección.

4. Cómo nuevas aplicaciones de la teoría de grafos sirven para cambiar de paradigma en nuestra comprensión de cómo se ensamblan los virus.

5. Cómo nuevos modelos matemáticos para el ensamblaje de virus sustentan el desarrollo de una terapia antiviral.

En cada uno de estos apartados, la autora desarrolla las ideas que hay detrás y los artículos en donde se encuentran los resultados.

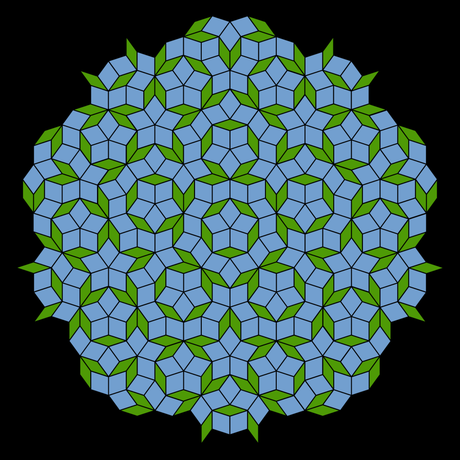
Una teselación de Penrose

Twarock conocía bien desde su tesis doctoral el mosaico de Penrose, y examinando la estructura del paporvaviridae, observó que mientras los virus icosaédricos agrupan sus proteínas en cápsides de cinco y seis, con un máximo de 12 grupos de 5, en este caso, hay 72 grupos de 5. El modelo de Twarock se asemejaba a un mosaico de Penrose envuelto alrededor de una esfera. Su descubrimiento permitió considerar no sólo la superficie del virus, como hasta entonces, sino su estructura tridimensional. Recordemos que estos patrones de las cápsides permiten ser generados como en las teselaciones simplemente preservando simetrías. La nueva visión tridimensional de Twarock supuso un avance extraordinario.

Concluimos esta entrada con una reflexión sobre la práctica inexistencia de investigadores y grupos de investigación con las características de Twarock, es decir, poseedores de una formación matemática sólida en campos como la biología y, en particular, la virología. Twarock originalmente estudió física y matemáticas en las universidades de Colonia y Bath, nada muy diferente a los bien establecidos dobles grados de varias de nuestras universidades. Su doctorado tampoco fue en biología, sino en modelos de confinamiento en mecánica cuántica, en la Universidad Técnica de Clausthal. Algo falta en nuestro sistema científico si no somos capaces de emular este tipo de investigación multidisciplinar.

Y les dejamos con una conferencia de Reidun Twarock

___________

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias) y Antonio Gómez Corral (Universidad Complutense de Madrid)