“Truco” para las razones trigonométricas de ángulos notables

En nuestra aventura de conocimiento que es la escuela, en esa travesía que hacemos por la senda de las matemáticas, que en ocasiones parece más un laberinto que un camino, llega un momento en que viajamos por el… mundo de la geometría.

Primero aparecen las figuras geométricas y aprendemos a distinguir entre triángulos, cuadrados, rectángulos, rombos y… ¡óvalos! Y además hacemos dibujos con ellos… la cabeza es un círculo, los brazos y las piernas son rectángulos, los pies triángulos…

Después aparecen otras figuras como los romboides, los trapecios, los trapezoides (que son algo así como los que no son nada de todo lo de antes)… hablamos de polígonos, y hacemos clasificaciones de todos ellos distinguiendo entre triángulos, cuadriláteros (y dentro de éstos paralelogramos, trapecios…)… aparecen los polígonos regulares de más de cuatro lados… y empezamos a calcular áreas y perímetros de todos ellos.

En fin, que parece que la cosa se va complicando, sobre todo si nos hemos perdido por el camino.

En ese mundo que se va levantando a nuestro alrededor la figura de los triángulos toma un papel destacado y, además, decimos que hay triángulos equiláteros, isósceles, escalenos, y también acutángulos, obtusángulos y… ¡rectángulos!

Sí… ¡rectángulos! (con exclamación) porque nos van a dar mucho juego. Buena culpa de ello la tiene la aparición estelar de… ¡El Teorema de Pitágoras!

Ese que dice que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo, sobre el que está tumbado el hipopótamo del dibujo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).

c² = a² + b²

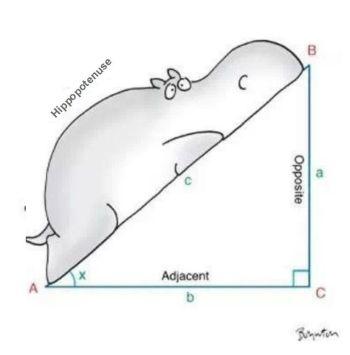
Sí porque, con el teorema de Pitágoras, los lados del triángulo rectángulo pasan a llamarse catetos e hipotenusa.

Al principio nos cuesta algo distinguir bien la hipotenusa (hay una extraña fuerza que nos atrae hacia el lado oscuro y nos hace pensar que debe ser el lado del que no conocemos su valor, comunmente conocido como “x”), pero llega un momento en que, de tantas veces que lo hemos visto, llegamos a controlarlo (más o menos)… y con ello, se despierta en nosotros una capacidad insospechada para calcular lados y alturas desconocidos en polígonos (sí, esos que nos hacen falta para las “fórmulas”)… ahora sí, parece que el cálculo de perímetros y áreas de figuras planas ya no se nos resiste (… o igual un poco).

Ilustración de Darth Vader, obra de Joe Wight. ¿Será éste el lado oscuro que nos hace pensar que la hipotenusa es siempre el lado que no conocemos?

Pero… lo que sí llevamos bien es eso de que los ángulos de un triángulo (que son tres) suman 180º. Y cuando no sabemos uno de ellos, le restamos a 180º los otros dos para calcularlo.

Nos decimos a nosotros mismos que parece sencillo lo de los ángulos. Además, también tenemos claro eso de que en el triángulo rectángulo hay un ángulo que es de 90º, y que se le llama ángulo recto.

Pero… entonces… aparece la… ¡Trigonometría!

Y empiezan a hablarnos de razones trigonométricas… de senos, cosenos, tangentes… ¡Pero esto qué es ahora!

Resulta que los lados del triángulo rectángulo ya no tienen sólo nombres, sino que también tienen apellidos: cateto opuesto y cateto contiguo o adyacente.

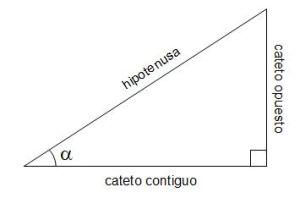
Así, aprendemos que el seno de un ángulo α es la razón entre el cateto opuesto a dicho ángulo y la hipotenusa…

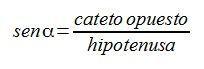
… el coseno de un ángulo α es la razón entre el cateto contiguo o adyacente a dicho ángulo y la hipotenusa…

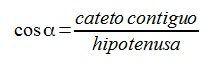
… y la tangente de un ángulo α es la razón entre el seno de dicho ángulo y su coseno o, expresado de otra manera, entre el cateto opuesto y el cateto contiguo…

Y no sólo eso, porque además están los inversos de cada uno de ellos y hay relaciones entre ellos… Incluso aparecen nuevas herramientas para el cálculo en triángulos, como el Teorema del seno y el Teorema del coseno….

… pero no nos adentremos tanto en este mar, porque para navegar en él habría que hacerlo más despacio y sabiendo lo que hacemos en cada momento.

Vamos a quedarnos en esto del seno y del coseno de un ángulo.

Resulta que cuando los estudiamos, aparecen una serie de ángulos que llamamos ángulos notables, que en el primer cuadrante nos cuentan que son 0º, 30º, 45º, 60º y 90º, y las razones trigonométricas de cada uno de ellos (eso del seno, coseno y tangente) tienen unos valores bastante particulares y que, además ¡tenemos que sabérnoslos!

…     …  …  …

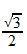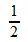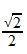En ese momento es cuando decimos ¿para qué?… ¡si seguro que me lo dice la calculadora!

Pero nuestra esperanza tecnológica rápidamente se desvanece cuando nos responden que debemos operar con fracciones y no con decimales, porque además de no perderse parte de la precisión con las aproximaciones que haríamos utilizando decimales, después se simplifican bastante las operaciones y nos van a quedar resultados “bonitos” (esos que cuando nos salen decimos: “esto seguro que está bien”).

Así es que, mucho que nos pese, tenemos que saber cuánto vale el seno, coseno y tangente de cada uno de estos ángulos.

Y aquí, después de todo este “sinuoso” recorrido, es donde interviene en nuestro auxilio (ya estábamos al borde de la desesperación) el “truco” al que hace mención el título de esta entrada.

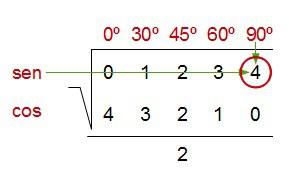
Si hiciésemos una tabla con los valores que se supone que debemos sabernos, sería algo así como la siguiente:

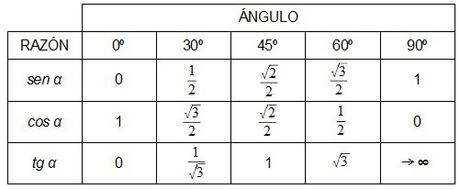
Ni que decir tiene que aprenderse los valores de la tangente es un poco absurdo pues, sabiendo el seno y el coseno, la tangente se obtiene dividiendo el primero entre el segundo. Con lo que nos valdría con aprendernos únicamente los valores del seno y del coseno.

Cuando tenemos una cosa así, solemos buscar un camino más sencillo que nos ayude a recordarlo. Es decir, intentamos crear una regla mnemotécnica. Pues eso es lo que vamos a hacer.

Primero dibujamos un símbolo de raíz grande, tal como éste…

… escribimos dentro dos filas de números, en la parte superior una que vaya del 0 al 4, y en la parte inferior otra que vaya al revés, del 4 al 0…

… dibujamos una barra grande debajo y un 2 bajo ella…

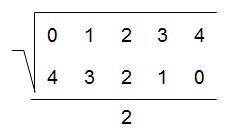
… y ahora lo completamos con lo que nos interesa saber…

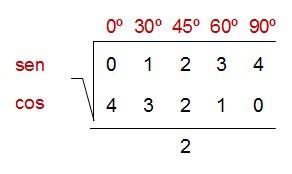
¡Pues ya lo tenemos!

Ya podemos saber el seno o el coseno de cualquiera de estos ángulos notables.

El procedimiento es bastante sencillo. El resultado va a ser la raíz de un número entre 2, y ese número es el que corresponde a la fila del sen o del cos (según queramos calcular el seno o el coseno) y a la columna del ángulo notable en cuestión. Después tan solo tenemos que simplificar el resultado obtenido, si se puede. Vamos a hacer unos ejemplos que así se ve mucho mejor.

Supongamos que queremos saber el sen 30º…

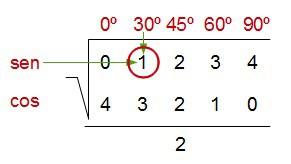
es decir:

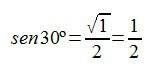
Calculemos ahora, por ejemplo, el cos 45º…

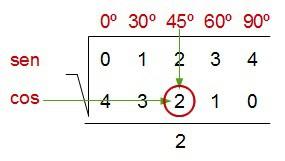
sería:

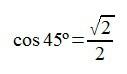
O el sen 60º…

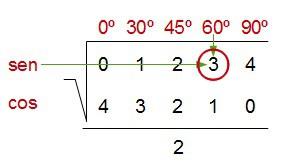
que es:

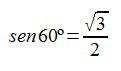
O el sen 90º…

es decir:

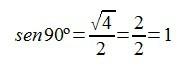
¿Sencillo, no?

Desde luego es una ayuda, y mejor que aprendérselas de memoria.

Pero ¿de verdad hay que aprendérselas de memoria?

Para mí el verdadero “truco” es saber deducirlas. Y mejor aún es hacerlo utilizando las cosas que ya conocemos.

Vamos a emplear el Teorema de Pitágoras y buscar triángulos rectángulos donde aparezcan estos ángulos notables.

¿En qué triángulo encontramos seguro ángulos de 60º? Pues en un triángulo equilátero, que tiene sus tres lados iguales y sus tres ángulos también iguales…

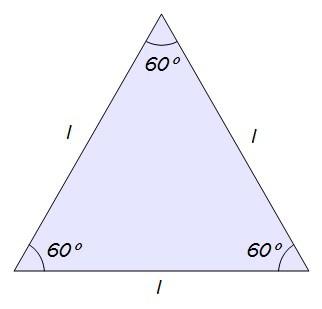
Pero, como lo que queremos es un triángulo rectángulo y además nos interesa encontrar también un ángulo de 30º, vamos a quedarnos con una de las dos mitades en que queda dividido por su altura…

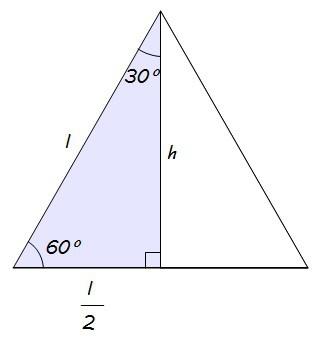
 Y ahora, para calcular el otro cateto que nos falta por saber (h), vamos a utilizar lo otro que habíamos comentado: el Teorema de Pitágoras.

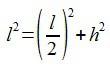
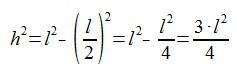
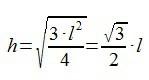
Ya sabemos todo lo que necesitamos para poder calcular las razones trigonométricas de 30º y 60º…

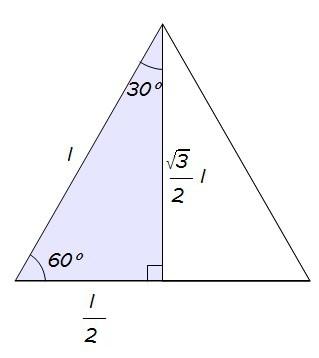
Lo hacemos:

Para ver ahora las razones trigonométricas de 45º, necesitamos un triángulo rectángulo que tenga un ángulo de 45º.

Si partimos de un cuadrado, de ángulos 90º…

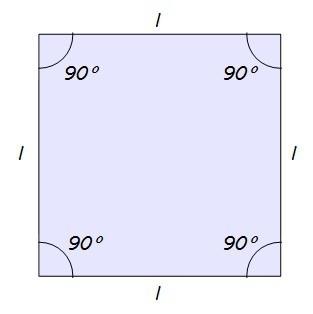
Y nos quedamos con una de las dos mitades en que queda dividido por una de sus diagonales, tenemos lo que buscábamos: un triángulo rectángulo con ángulos de 45º…

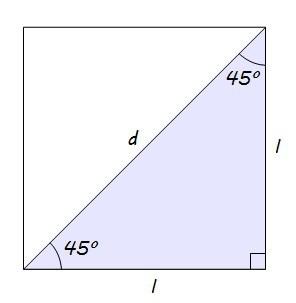
En este caso, lo que nos falta por averiguar es la hipotenusa (d), para lo que volvemos a utilizar el Teorema de Pitágoras.

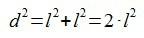
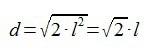
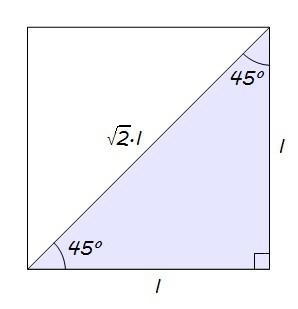Y ya podemos calcular el seno y el coseno de 45º:

Nos quedan por ver las razones trigonométricas de 0º y 90º. En ambos casos tenemos que recurrir a “triángulos teóricos”. Vamos a verlo.

Si partimos de un triángulo rectángulo con un ángulo cualquiera, y vamos disminuyendo cada vez más ese ángulo, como se ve en la siguiente imagen, el cateto opuesto se va haciendo cada vez más pequeño y la longitud del cateto contiguo se acerca cada vez más a la longitud de la hipotenusa. Así, cuando el ángulo es de 0º, tenemos un “triángulo teórico” en el que el cateto opuesto es cero y el cateto contiguo coincide con la hipotenusa.

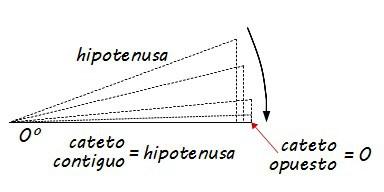
De esa manera el seno y el coseno de 0º serían:

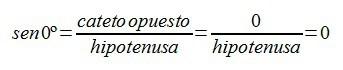
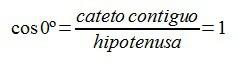
Si partimos ahora de un triángulo rectángulo con un ángulo cualquiera agudo, y vamos aumentando cada vez más ese ángulo acercándonos a 90º, el cateto contiguo se va haciendo cada vez más pequeño y la longitud del cateto opuesto se acerca cada vez más a la longitud de la hipotenusa. De esa manera, cuando el ángulo es de 90º, se tiene un “triángulo teórico” en el que el cateto contiguo es cero y el cateto opuesto coincide con la hipotenusa.

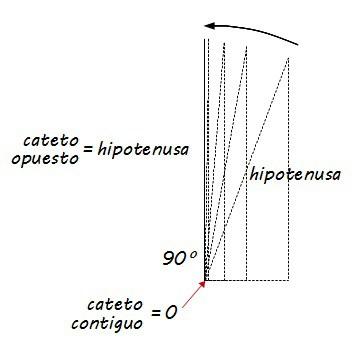
Y en esa situación:

Pues ya tendríamos el seno y el coseno de los ángulos notables del primer cuadrante.

¿Y la tangente? Pues lo que habíamos dicho ya: dividiendo directamente el seno entre el coseno.

Como conclusión, es práctico tener un “truco” o regla mnemotécnica como el que hemos visto, pues nos permitirá saber con bastante rapidez el valor de las razones trigonométricas que necesitemos cuando estemos haciendo cálculos.

Pero es muy importante saber de dónde vienen estos valores y tener bien claros los conceptos, en definitiva, entender las cosas, porque es lo que nos va a permitir hacer mucho más y, como diría el Maestro Yoda, “de bastantes situaciones airosos salir”.

Ilustración realizada por Joe Wight de Yoda.

¡Qué la fuerza os acompañe!

 Esta entrada participa en la Edición 6.X “El grafo” del Carnaval de Matemáticas, cuyo anfitrión es el blog Cifras y Teclas.