UCB1 para un problema Bandido Multibrazo (Multi-Armed Bandit)

Las diferentes estrategias que hemos visto hasta ahora para resolver un problema tipo Bandido Multibrazo (Multi-Armed Bandit) se basan en la exploración aleatoria de los estados, como puede ser el caso de Epsilon-Greedy, o en un conocimiento previo de los mismos, como es el caso de valores iniciales optimistas. Lo que puede ser problemático en ciertas ocasiones. Epsilon-Greedy puede explorar opciones que no son óptimas tras observar valores atípicamente altos o bajos para un bandido. Mientras que en valores iniciales optimistas puede que el conocimiento previo que se tiene no sea el correcto, lo que puede llevar a no explorar algunos estados. UCB (Límite de Confianza Superior, del inglés Upper Confidence Bounds) es una familia de algoritmos en los que se estima un límite de confianza superior para determinar cuál es la mejor optima. En esta ocasión nos vamos a centrar en la implementación de UCB1 para un problema Bandido Multibrazo.

La desigualdad de Hoeffding

En el caso de que no queramos asumir ningún supuesto sobre la distribución de las recompensas de los bandidos se puede usar la desigualdad de Hoeffding. Una desigualdad que se puede aplicar a cualquier distribución. La desigualdad de Hoeffding indica la probabilidad de que la suma de un conjunto de valores aleatorios se desvíe de su valor esperado. Una desigualdad que se puede expresar de la siguiente forma

Pr\left(\left|\bar{X_j} - \mu_j\right| \ge \varepsilon \right) \le 2 e^{-2 n_i \varepsilon^2}

donde \bar{X_j} es la media de los valores para el bandido j, \mu es la media del bandido j, \varepsilon es el valor máximo para el que queremos medir la probabilidad y n_j es el número de muestras. Con lo que es posible estimar el intervalo de confianza que podíamos esperar para para una probabilidad alpha.

\varepsilon_j = \sqrt{\frac{1}{2n_j} ln{\frac{2}{\alpha}}}

UCB1

Un método heurístico para la determinación de la probabilidadalpha es que esta se reduzca con el tiempo. Al principio sea menos estricto, pudiendo explorar más, pero a medida que aumenta el número de datos ser más estrictos. En el caso de UCB1 se fija el criterio como

\frac{\alpha}{2} = N^{-4}

donde N es el número total de tiradas en los todos los bandidos. Con lo que el intervalo de confianza para el bandido j queda de la siguiente forma:

\varepsilon_j = \sqrt{\frac{2 log{N}}{n_j}}

Ahora, el algoritmo UCB1 seleccionará en cada momento el bandido cuya recompensa esperada junto con su intervalo de confianza devuelva el valor más elevado. Esto es, se seleccionará el bandido en base a la siguiente expresión:

X_{UCB1{j}} = \bar{X_j} + \sqrt{\frac{2 log{N}}{n_j}}

Implementación de UCB1 en Python

Ahora que conocemos la fórmula con la que se selecciona el bandido mediante UCB1 se puede modificar la clase Epsilon que hemos utilizado anteriormente. Para lo que se tendrá que modificar el método select() para que use USB1 como criterio de selección. Lo que se puede ver en el siguiente código.

class UCB(Epsilon):
    def __init__(self, bandits):
        self.bandits = bandits
        
        self.reset()
    
    def select(self):
        num_bandits = len(self.bandits)
        total = len(self._rewards)
        
        if total == 0:
            bandit = np.random.choice(len(bandits))
        else:
            ucb = [0] * num_bandits
            
            for i in range(num_bandits):
                if self._plays[i] == 0:
                    ucb[i] = self._mean[i] + np.sqrt(2 * np.log(total))
                else:
                    ucb[i] = self._mean[i] + np.sqrt(2 * np.log(total) / self._plays[i])
        
            max_bandits = np.where(ucb == np.max(ucb))[0]
            bandit = np.random.choice(max_bandits)
            
        return bandit
    
    
    def reset(self, initial=None):
        self._rewards = []
        self._plays = [0] * len(self.bandits)
        self._mean = [0] * len(self.bandits)

Únicamente se ha tenido en cuenta dos cosas, la primera jugada, cuando el valor de total es cero, se tiene que hacer aleatoriamente. Posteriormente, el valor de usb se calcula para cada bandido, evitando la división por cero en las primeras tiradas.

Al igual que en ocasiones anteriores, cuando se observa un empate, se decide el bandido con el que se juega de forma aleatoria.

Resultados de UCB1

Para evaluar el rendimiento de este algoritmo se puede usar la clase Bandit basados en una distribución binomial empleada anteriormente. Usando para ello el suficiente código

np.random.seed(0)

bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)]

ucb_1 = UCB(bandits)
ucb_1.run(20000)
ucb_1.plot(True, True, label='UCB-1')
plt.legend()

Lo que nos genera el siguiente resultado.

Evolución de la recompensa promedio con el numero de tiradas para el algoritmo UCB1 con tres bandidos basados en una distribución binomial

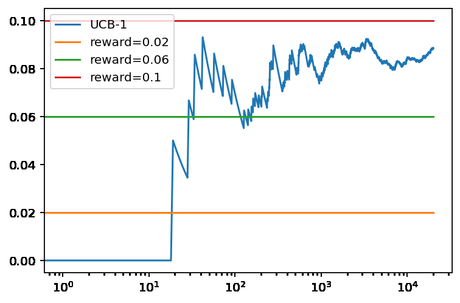
Vemos que UCB-1 se decanta bastante rápido por el bandido óptimo. Aunque en este caso, debido a que los valores de las recompensas están bastante cerca, realiza muchas jugadas con el bandido que no es óptimo. Lo que produce que la recompensa promedio que obtiene este más cercano al valor del bandido con mayor recompensa real. Algo que sí pudimos observar en el caso del método basado en Softmax.

Conclusiones

En esta entrega hemos visto cómo utilizar UCB1 para un problema Bandido Multibrazo. Un algoritmo que se basa en la desigualdad de Hoeffding para obtener un intervalo de confianza para la recompensa de cada uno de los bandidos. Seleccionando de este modo el bandido cuya recompensa observada más el intervalo de confianza sea máximo. En futuras entregas veremos otras versiones de este algoritmo como es UCB2 o UCB-Normal.

Imagen de pasja1000 en Pixabay