UCB1-Tuned para un problema Bandido Multibrazo (Multi-Armed Bandit)

La semana pasada hemos visto UCB2, un algoritmo que ha ofrecido mejores rendimientos que UCB1 para nuestros bandidos basados en una distribución binomial. En esta ocasión vamos a ver UCB1-Tuned (también conocido como UCB-Tuned), una mejora de UCB1 en el que se modifica la fórmula con la que se calcula el límite de confianza superior.

UCB1-Tuned

El método UCB1-Tuned propone una mejora estricta de la expresión usada en UCB1 para determinar el límite de confianza superior para cada uno de los bandidos. Modificando de esta manera la regla de selección. En concreto, lo que se hace es modificar la formula para el cálculo de

\varepsilon_j = \sqrt{\frac{2 \log N}{n_j}},

donde N es el número total de veces que se ha jugado con un bandido y n_j las que se ha jugado con el bandido j. Reemplazandola por la expresión

\varepsilon_j = \sqrt{\frac{\log N}{n_j} \min(1/4, V_j(n_j))},

donde V_j es una estimación de límite confianza superior que se puede obtener mediante

V_j(n_j) = \bar{X_j^2} - \bar{X_j}^2 + \sqrt{\frac{2 \log N}{n_j}},

en donde \bar{X_j^2} es la media de los cuadrados de las recompensas y \bar{X_j} es la media de las recompensas.

El algoritmo UCB1-Tuned suele superar empíricamente a UCB1 en cuanto a la veces que selecciona el mejor bandido. Además de ser un método menos sensible a la variabilidad de las recompensas.

Implementación de UCB1-Tuned en Python

Al igual que en las entradas anteriores vamos a realizar una implementación de UCB1-Tuned en Python. Para lo que nos basaremos en la clase Epsilon implementada para al hablar de Epsilon-Greedy. Siendo necesario en esta ocasión modificar los método run(), select() y reset(), además de agregar la propiedad privada _mean2. Cambios que se muestran en el siguiente código.

class UCB1Tuned(Epsilon):
    def __init__(self, bandits):
        self.bandits = bandits
        
        self.reset()
    
    
    def run(self, episodes=1):
        for i in range(episodes):
            # Selección del bandido
            bandit = self.select()
            
            # Obtención de una nueva recompensa
            reward = bandits[bandit].pull()
            
            # Agregación de la recompensa al listado
            self._rewards.append(reward)
            
            # Actualización de la media
            self._plays[bandit] += 1
            self._mean[bandit] = (1 - 1.0/self._plays[bandit]) * self._mean[bandit] \
                                 + 1.0/self._plays[bandit] * reward
            
            # Actualización de la media de los cuadrados
            self._mean2[bandit] = (1 - 1.0/self._plays[bandit]) * self._mean2[bandit] \
                                 + 1.0/self._plays[bandit] * reward ** 2
        
        return self.average_reward()
    
    
    def select(self):
        num_bandits = len(self.bandits)
        total = len(self._rewards)
        
        if total == 0:
            bandit = np.random.choice(len(bandits))
        else:
            ucb = [0] * num_bandits
            
            for i in range(num_bandits):
                if self._plays[i] == 0:
                    v = self._mean2[i] - self._mean[i] ** 2 + np.sqrt(2 * np.log(total))
                else:
                    v = self._mean2[i] - self._mean[i] ** 2 + np.sqrt(2 * np.log(total) / self._plays[i])
        
                ucb[i] = self._mean[i] + np.sqrt(np.log(total) * np.min([1/4, v]))
            
            max_bandits = np.where(ucb == np.max(ucb))[0]
            bandit = np.random.choice(max_bandits)
            
        return bandit
    
    
    def reset(self, initial=None):
        self._rewards = []
        self._plays = [0] * len(self.bandits)
        self._mean = [0] * len(self.bandits)
        self._mean2 = [0] * len(self.bandits)

La propiedad privada _mean2 es necesaria ya que es necesario disponer de la media de los cuadrados de cada uno de los bandidos. Una propiedad que se puede calcular como _mean reemplazando la recompensa por la recompensa al cuadrado. Propiedad que se tiene que reiniciar mediante el método reset().

Para actualizar el valor de _mean2 es necesario incluir el cálculo de esta propiedad en el método run(). Lo que se ha hecho utilizando la misma expresión para actualizar el valor que la media. Siendo este el único cambio implementado en run().

Finalmente, el método select() se tiene que actualizar con la nueva fórmula para seleccionar el límite de confianza superior y, en consecuencia, la selección del bandido con el que jugar en cada momento.

Resultados de UCB1-Tuned en Python

Al igual que en las entradas anteriores se puede ver el rendimiento de este método. Para ello se pueden utilizar la clase Bandit creada en la entrada de valores iniciales optimistas. Una clase que implementa unos bandidos basados en la distribución binomial. Así para probar el algoritmo y compararlos con UCB1 solamente se tienen que escribir el siguiente código.

np.random.seed(0)

bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)]

ucb_tuned = UCB1Tuned(bandits)
ucb_1 = UCB1(bandits)

ucb_tuned.run(200000)
ucb_1.run(200000)

ucb_tuned.plot(True, label='UCB-Tuned')
ucb_1.plot(True, True, label='UCB-1')
plt.legend()

Lo que genera la siguiente gráfica.

Evolución de la recompensa promedio con el numero de tiradas para el algoritmo UCB1 y UCB1-Tuned con tres bandidos basados en una distribución binomial

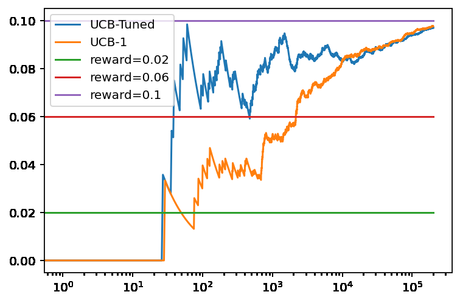
Lo que se puede ver en este ejemplo es que el rendimiento de ambos métodos es similar a largo plazo, convergiendo ambos hacia valores muy próximos al teórico del mejor bandido. Aunque el método UCB1-Tuned ha detectado el bandido óptimo más rápido que UCB1. Por lo que demuestra ser un método más adecuado cuando el número de tiradas disponibles es reducido.

Conclusiones

En esta entrada hemos visto un tercer método de la familia UCB (Límite de Confianza Superior, del inglés Upper Confidence Bounds) para resolver un problema tipo Bandido Multibrazo. Concretamente el método UCB1-Tuned. Siendo este una mejora de UCB1 que, en el ejemplo que hemos visto, reconoce más rápidamente el bandido óptimo. Aunque quedan por ver más métodos UCB cómo pude ser el que veremos la semana que viene: UCB-Normal.

Imagen de Giani Pralea en Pixabay