Un sistema de ecuaciones diferente

A veces en Descubrir La Química hacemos alguna entrada haciendo el análisis de algún ejercicio a medida que lo resolvemos. Hoy en concreto vamos a hacer el análisis de un sistema de ecuaciones que me preguntó una alumna a la que le di clases este año de Matemáticas I de primero de Bachillerato. El sistema es el siguiente:
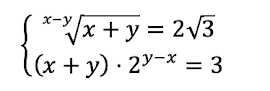Es un sistema que se sale de las clasificaciones habituales ya que no es:-Un sistema de ecuaciones exponenciales.-Un sistema de ecuaciones logarítmicas.-Un sistema de segundo grado.-Un sistema para hacer por Gauss.-Un sistema para hacer por sustitución, reducción o igualación.

Que son los casos principales que se han trabajado hasta primero de bachillerato ¡Por lo menos a simple vista!Entonces ¿Cómo lo hacemos? ¡Podemos tomar logaritmos en la segunda ecuación! Ya que tiene pinta de exponencial. Pero ¿Hemos arreglado algo? Si probamos a hacerlo vemos que no mucho.Ahora viene lo bueno, en la primera ecuación tenemos raíz con exponente x-y. Normalmente, si por ejemplo tenemos una raíz cuadrada, elevamos todo a dos; si tenemos una raíz cúbica elevamos todo a 3; teniendo raíz con exponente x-y ¿Por qué no elevar a ambos lados a la potencia x-y? Y esto nos lleva a:

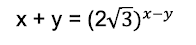¡Hemos despejado x + y! Si nos fijamos, esto podemos sustituirlo en la ecuación de abajo y entonces nos queda: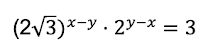
Y ahora vamos a expresar la raíz de 3 como:

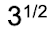
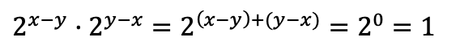
Si elevamos el paréntesis a x-y, esto nos queda:

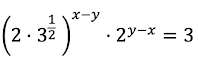
Aplicando las propiedades de las potencias:
Entonces, tenemos:
Y ahora, tenemos una ecuación exponencial, en la que como ambos miembros tienen la misma base igualamos los exponentes. Recordemos que 3 es lo mismo que 3 elevado a 1.

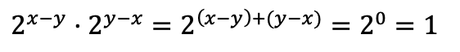
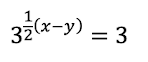
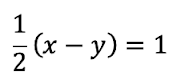
El 2 que está dividiendo pasa multiplicando:

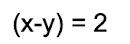
Volvemos a:
Sustituimos x en ella:
Y como:

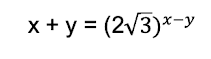
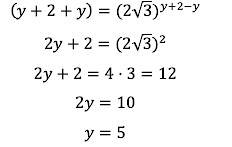
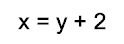
Por lo tanto, las soluciones del sistema son:

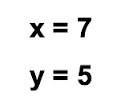
Analicemos el problema:Empezamos aplicando propiedades de las potencias, pero en lugar de trabajar con números, lo hicimos con letras. Después utilizamos el método de sustitución, aunque no despejamos directamente x o y, sino x + y, y lo sustituimos en la otra ecuación. El sistema se redujo a una ecuación exponencial sencilla que nos permitió hallar x, y finalmente llegamos a una ecuación de primer grado que nos dio y.
A veces, problemas que a primera vista parecen complicados se reducen a algo simple: solo hay que encontrar la clave adecuada.
22/07/2025Aida Amor Cañoto López. Profesora de Ciencias en Centro de Estudios NEOS.