Una para “nerds”

Ha sido un verano muy curioso. Hace una semana que ya concluí mi curso especial (con derecho de autor y todo) de Cálculo que imparto todos los veranos a cualquier universidad americana que me acoja. Leyendo los comentarios de los alumnos en sus “evaluaciones” de mí, muchos dijeron que fue uno de sus mejores veranos en toda la vida, que yo les “inspiré” y demás cosas bonitas en las que no me voy a centrar. Entre las críticas, no obstante, dijeron que el curso es “muy difícil”, “demasiado riguroso” y que yo no tengo en cuenta que son “jóvenes” que en muchas ocasiones no alcanzan ni los 20 años. ¡Como si eso fuera pretexto para degenerar y degradar la calidad de las clases! El decano, por su parte, me dio la mano y me ha otorgado un certificado como “el mejor profesor de cursos de verano” que tuvo la Universidad de Miami este verano. “Gracias don Alfredo, por elevar la calidad de nuestras clases” y obligar a los estudiantes a pensar más allá de sus límites. Nunca se olvidarán de ti”, dice el decano en su carta dirigida a mí. No, tranquilos – no se ha traducido en un empleo ni en un contrato indefinido, que en EEUU tampoco atan los perros con longaniza y el esfuerzo ya no cuenta tanto como hace décadas. Pero esta entrada va a ser exclusivamente matemática, así que si no entiendes mucho del tema, posiblemente no te vas a enterar de mucho hoy. Por eso la he titulado “para nerds”. En mi época colegial, yo oscilaba entre la “tribu urbana” de los “nerds” (sobre todo al principio) para luego convertirme en una suerte de “pijo” pensador, eso sí, siempre riguroso en mi análisis. ¿Por qué ha sido tan “riguroso” mi curso de Cálculo? Por mi filosofía sobre cómo se “debe” impartir el Cálculo en la universidad. ¿Cuál es ese método? El infinitesimal. ¿Qué es? Cito de la wikipedia: “El cálculo infinitesimal fue propuesto inicialmente por Arquímedes. Luego fue utilizado por Isaac Newton y Gottfried Leibniz, en los albores del surgimiento del Análisis matemático moderno, pero posteriormente fue desacreditado por George Berkeley y finalmente olvidado. Durante el siglo XIX Karl Weierstrass y Cauchy comenzaron a utilizar la definición formal de límite matemático, por lo que el cálculo infinitesimal ya no era necesario. Sin embargo durante el siglo XX los infinitesimales fueron rescatados como una herramienta que ayuda a calcular límites de forma simple.” Es un método completamente riguroso. Debo decir (esto lo entenderán los que han estudiado las controversias en las matemáticas) que personalmente soy fanático — rozando el sectarismo, del método de Leibniz, el alemán, por encima del inglés, Newton. El cálculo de Leibniz es riguroso, mucho más analítico y estricto en normas que el de Newton.

Para comparar, normalmente los estudiantes de cálculo (al menos en EEUU, desconozco el caso español actual) aprenden la definición famosa del límite: ε – δ. Aún cuando se dedica muchísimo tiempo a esta definición, la mayoría de estudiantes no lo aprende correctamente. Es más, en la mayoría de cursos, le dedican poco tiempo. Por esta falta de comunicación, porque se imparte mal, el estudiante se ve privado de un cálculo — un método para calcular que ha funcionado bien durante siglos y es totalmente riguroso.

Aquí van algunos ejemplos de lo que un estudiante podrá hacer después de estar en mi clase.

a ≃ b significa que a – b es infinitesimal; por ejemplo, a ≃ 0 significa que “a” es infinitesimal. Si “r” es real
y a ≃ r, podemos escribir que r = st (a) (la parte estándar de “a”). Claro, si a y b son reales y a ≃ b, entonces
a = b. Déja que y = f(x) y Δy = f(x + Δx) – f(x). Por definición, f es una función continua en todo x porque (x + Δx)² = x² + 2xΔx + Δx² ≃ x² cuando Δx ≃ 0. Resumiendo, todo esto queda así finalmente:

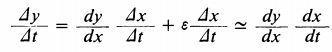
A menudo, esta prueba se ignora, probablemente debido a la aversión que existe contra el método antiguo de los infinitesimales.

Otros ejemplos –

Funciones

Deja que “h” sea la siguiente función:

h(t) = t³ + 1

t es una variable, h es una función, y h(t) es un término algebraico. Las siguientes expresiones también son términos y se computan con el método de la sustitución:

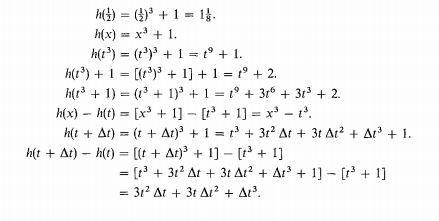
Si dibujamos h(t) = t³ + 1 con unos puntos, tenemos esto:

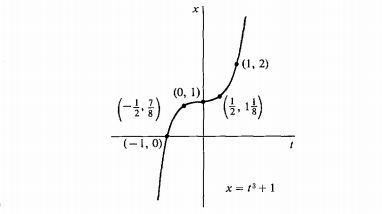
Quizás la mejor descripción para el curso que ofrezco es simplemente CÁLCULO. Me dedico exclusivamente al cálculo en la asignatura, nunca mezclo temas ni degrado los temas solo para que TODOS puedan entenderlo (aunque en realidad eso es imposible). Es posible que yo sea un poco psicópata en algunos temas, pero pienso que si no estás sufriendo en una clase de cálculo, probablemente no te están enseñando cálculo realmente.

Muchos libros de texto modernos no explican la materia, sólo ofrecen herramientas para resolver problemas y “aplicaciones” de cálculo como dicen, para aprobar exámenes nacionales. Eso está muy bien para los que no les interesa nada las matemáticas, pero no me vale para ENSEÑAR CALCULO. Mis apuntes no están tupidos de gráficas generadas por ordenadores ni por ejemplos redundantes. Ofrezco pruebas y teoremas para justificar lo que hacemos. Mi rigor no tiene límites.

Eso sí, mis apuntes no son para los blanditos que solo quieren aprobar y salir del tema. Si solo te interesa resolver problemas de calculo, no durarás mucho en mi clase. Pero si quieres las herramientas y las justificaciones detrás de las respuestas, entonces te gustará mi curso de verano.

Estoy absolutamente centrado en la escuela de Weierstrass. A los alumnos no les gusta tantas letras griegas, tantas deltas, tantas pruebas, pero para mí, sin eso, no hay justificación alguna para aprender.

El calculo debería ser comparable a una serie de latigazos que te escarmientan a comportarte y ser mejor persona. Siento pasión por la asignatura, pureza en mi prosa y cierto rigor de fanatismo, lo reconozco. Es que me da pasión cada vez que los alumnos y yo resolvemos una ecuación después de sudar mucho por los nervios que generan los ejercicios difíciles. Los reaccionarios detestan mi forma de impartir la asignatura y prefieren las matemáticas aplicadas, pero yo creo que los jóvenes aprenden más en mi clase – no, no lo digo por ser arrogante sino por lo que me dicen ellos mismos.

Mis apuntes y formas de dar la clase no son del agrado de todos. Se presupone que tengas cierto rigor. Si no lo tienes, lo pasarías muy mal en mi clase.

Termino con el texto de una evaluación de un alumno en clase:

“La verdad es que esta clase ha sido la más difícil que he tenido en toda mi vida. Tuve que pasar horas y horas solamente en tres problemas. Horas. A veces tenía éxito, en la mayoría de ocasiones sentí frustración con el profesor y sus métodos. Entonces se me ocurrió preguntarle en tutorías o por la calle, a ver si me atendía y así fue. Alfredo es un gran defensor de la memorización de teoremas, pero a mí me ayudó mucho y se implicó en mi vida personal. Nunca me dio respuestas porque me decía que “yo soy capaz” de encontrar la solución, pero sí me ofrecía marcos para intentarlo. Aun con todos mis esfuerzos, solo consegui una “B” (notable, en España). Me sentí muy decepcionado porque realmente quería un sobresaliente. Pero Alfredo me dijo que debo tener perspectiva. Al final del curso, tenía un nivel muchísimo más alto que mis compañeros en otra clase con otro profesor más moderno que Alfredo. Los logaritmosya no me intimidaban. No exagero cuando digo que si conseguiste un “notable” de este profesor, podrías impartir una clase de cálculo físico si usas los libros normales en EEUU. Si te gusta sufrir pero aprender al final, debes apuntarte a las clases de este señor porque su método es el más riguroso”.