Señores: Antes de entrar al tema, he visto que tengo montones de comentarios pendientes de respuesta. En las últimas semanas han pasado muchas cosas que me han impedido entrar aquí con calma y tiempo. Entre ellas, una tormenta tropical (gracias, calentamiento global provocado por el ser humano) y en consecuencia cortes de luz que duraron días y mostraron que Estados Unidos no sólo ya es un “emperador desnudo” al mundo, sino que la infraestructura nacional es tercermundista. Ni siquiera en la República Dominicana duraría más de 1 semana el corte de luz por una tormentita que ni siquiera duró 15 minutos. No hubo ni vientos que justificaran el apagón masivo en gran parte del estado de New Jersey y Nueva York…pero en fin, en esas estamos. Por otro lado, tuve un psicópata ex-inquilino amenazando mi vida y tuve que estar armado y preparado. Posteriormente, me dijo que se iba a “suicidar”. No he vuelto a oír nada, así que supongo que, o bien cumplió su amenaza, o bien se dio cuenta ante mi falta de respuesta y perder mi tiempo que patalear no funciona conmigo.
Me comprometo con responder a todo el mundo entre hoy y este fin de semana, incluido el largo comentario del lector IOSEFF…le debía una respuesta y a mí no se me olvidan las cosas.
——————————————————————
Entremos, pues, al asunto de hoy que me chocó bastante el otro día. Se trata de una de las preguntas matemáticas en el examen de oposición para profesores de matemáticas para Valencia, España, año 2019.
La pregunta es la siguiente:
Demostrar que el volumen de cualquier cono recto inscrito en una esfera es menor que el 30% de la esfera. Si quieren ver una solución al problema (porque este mismo ejercicio se publicó en el examen de selectividad de 2005), aquí hay una solución de Segundo Pérez (ingeniero).
Copio la solución que aportó otro ingeniero — Jose Antonio Álvarez Cubero. Posteriormente, os demostraré como matemático puro, una solución mucho menos liosa y más elegante, en términos de matemáticas puras.
——————————-
SOLUCIÓN DE ÁLVAREZ CUBERO:
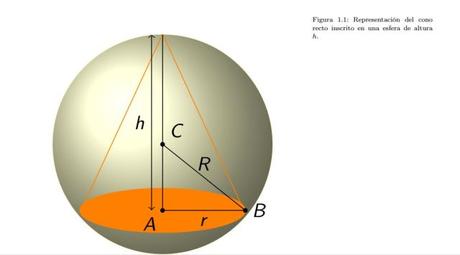
Consideramos una esfera de radio fijo R. Encontraremos un cono recto La distancia desde el vértice hasta el plano que contiene la base es la altura h del cono. El radio de la base se llama radio r del cono. Si el vértice está situado en la vertical trazada desde el centro de la base, llamamos al cono un cono circular recto, o simplemente, cono recto. de volumen máximo que se pueda inscribir en la esfera en función de R y el radio r y altura h del cono.
La distancia desde el vértice hasta el plano que contiene la base es la altura h del cono. El radio de la base se llama radio r del cono. Si el vértice está situado en la vertical trazada desde el centro de la base, llamamos al cono un cono circular recto, o simplemente, cono recto.
1.2.1 Método maximizando la altura del cono
El volumen de un cono viene dado por:
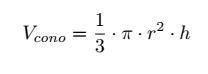
Como podéis ver, es una solución innecesariamente engorrosa, pero muy representativa del estílo de un ingeniero. He de reconocer que es una respuesta formal y elegante. No tiene nada “mal”, pero yo prefiero resolver los problemas desde una óptica más puramente matemática.
—————————————————-
MI SOLUCIÓN:
Vamos a permitir que el ápice del cono se encuentre en el punto (-1, 0, 0) y dejemos que su base esté situada en el plano de coordinadas z = c.
Entonces, el área de la base es:
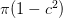
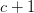
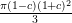
Si tomamos la derivada de esto y controlamos para que el resultado sea cero, llegamos a producir la siguiente ecuación:
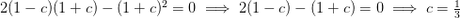
El volumen del cono cuando
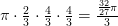
Si dividimos esto por
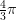
Problema resuelto.
¿Qué solución os ha gustado más y por qué?
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure