Una prueba alternativa de la derivada del producto

Una de las reglas de derivación que más se utilizan es la derivada de un producto de funciones. Creo que todo estudiante de bachillerato la conoce:

Pero quizás lo que se vea menos es la demostración de esta propiedad. Y quizás la razón es que es poco intuitiva (para un alumno de bachillerato o primer curso de una carrera científico-técnica). La demostración estándar la podéis encontrar en la wikipedia, por ejemplo. Aquí os traigo otra demostración mucho más sencilla e intuitiva que he encontrado a través de Facebook (siento no tener el enlace).
Vamos allá.
En primer lugar, vamos a demostrar que y lo vamos a hacer por fuerza bruta, usando la definición de derivada como límite de cocientes incrementales.

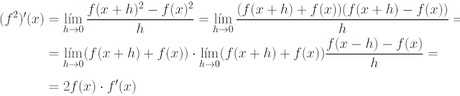
Bien, una vez que sabemos  derivar cuadrados (que en el fondo es un caso particular de un producto), podemos pasar al caso general. Para ello, podemos actuar de 2 maneras.
En la primera, consideramos la función y la tratamos de derivar. Resulta que, aplicando la regla del cuadrado, tenemos que

 pero desarrollando previamente el cuadrado y luego derivando, tenemos que

Y comparando ambos resultados se tiene la regla del producto.
También podríamos haberla derivado sin más que darse cuenta de que , por lo que
.
Espero que esta forma os resulte algo más intuitiva. A mí, particularmente, sí.
Referencias:
Piotr Josevich, An Alternative Approach to the Product Rule, American Mathematical Monthly 123 (2016), 470.
Tito Eliatron Dixit
PD: Esta entrada participa en la edición 7.4 del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews.  
 
Esta entrada se ha publicado originalmente en Tito Eliatron Dixit.
Si la estás viendo en otra web, probablemente estéás siendo víctima de un engaño.