
Nivel IV: Otras estructuras matemáticas
Las condiciones iniciales y constantes físicas en los multiuniversos de Nivel I, II, y III pueden variar, pero las leyes fundamentales de la Naturaleza permanecen. ¿Por qué vamos a pararnos ahí?. ¿Por qué no consentimos que las mismas leyes varíen? ¿Un universo que obedece las leyes de la física clásica, sin efectos cuánticos? ¿Un tiempo que transcurre en intervalos, como en los ordenadores, en lugar de ser contínuo?. ¿Un universo que no sea más que un dodecaedro vacío?. En el multiuniverso de nivel IV existen todas esas alternativas.
Según el paradigma aristotélico, la realidad física es fundamental y el lenguaje matemático, una mera aproximación útil. Según el paradigma platónico, la estructura matemática es la verdadera realidad y los observadores la perciben de manera imperfecta. En otras palabras, los dos paradigmas discrepan en qué perspectiva de las leyes físicas es más fundamental, la de la rana o la del pájaro.
El paradigma aristotélico prefiere la perspectiva de la rana, mientras que el platónico se queda con la del ave. Desde niños, desde mucho antes de que hubiésemos siquiera oído hablar de matemáticas, se nos adoctrinó en el paradigma aristotélico. El punto de vista platónico es un gusto adquirido. Los físicos teóricos modernos tienden a ser platónicos: sospechan que las matemáticas describen tan bien el universo porque el propio universo es matemático.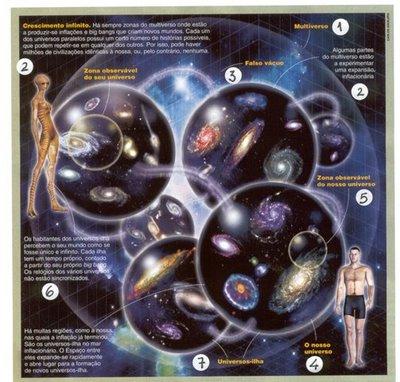
1 - El Multiverso (conjunto de universos múltiples)
2 - Crecimiento infinito - siempre hay áreas en el multiverso donde se produciran grandes explosiones que crean nuevos mundos. Cada uno de los universos paralelos tiene una serie de historias posibles, que se puede repetir en cualquier otro. Así que puede haber millones de civilizaciones similares a la nuestra, o, por el contrario, no.
3 - Falso vacío (espacio en el que puede elevarse nuevos universos)
4 - Nuestra zona de Universo
5 - Nuestro universo observable
6 - Los habitantes del universo de las islas perciben su mundo como uno e infinito. Cada isla tiene un tiempo propio, a partir de su propio Big Bang.
7 - Universos islas.
Luego la física entera es en sí un problema de matemáticas: un matemático con una inteligencia y unos recursos ilimitados podría en principio calcular la perspectiva de la rana; es decir, calcular qué observadores conscientes de sí mismos contiene el universo, qué perciben y qué lenguajes se inventan para describirse sus percepciones unos a otros.
Una estructura matemática constituye un ente abstracto e inmutable que existe fuera del espacio y del tiempo. Si la historia fuese una película, la estructura correspondería, no a un solo fotograma, sino a la cinta completa.
Considere, por ejemplo, un mundo hecho de partículas puntuales que se muevan en el espacio tridimensional. En el espacio-tiempo tetradimensional -la perspectiva del pájaro- esas trayectorias de las partículas parecen una maraña de espaguetis. Si la rana ve una partícula moviéndose con velocidad constante, el pájaro ve un espagueti recto. Si la rana ve un par de partículas en órbita, el pájaro ve dos espaguetis entrelazados como una hélice doble. Para la rana, el mundo está descrito por las leyes de Newton sobre el movimiento y la gravitación. Para el pájaro, está descrito por la geometría de la pasta, una estructura matemática. La rana misma es un grueso manojo de pasta, cuyo complejo entrelazado corresponde a un cúmulo de partículas que almacenan y procesan información. Nuestro universo es mucho más complicado que este ejemplo, y los científicos no saben todavía a qué estructura matemática corresponde, suponiendo que corresponda a alguna.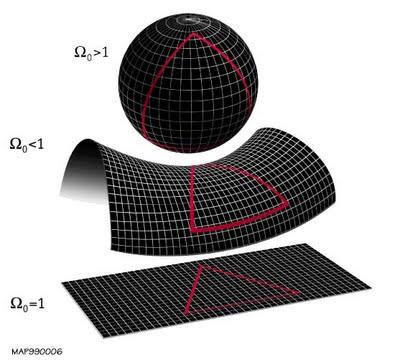
En los tres casos vemos que el universo en definitiva, no es infinito si no todo lo contrario, es finito. Lo que es infinito es el espacio.
El paradigma PLATONICO suscita la pregunta de por qué el universo es como es. Para un ARISTOTELICO la pregunta carece de sentido: el universo simplemente es. Pero un platónico no puede evitar preguntarse por qué no podría haber sido diferente. Si el universo es en sí matemático, entonces ¿por qué sólo se escogió una estructura matemática entre muchas para describir un universo? Parece que una asimetría fundamental forma parte inseparable de las raíces mismas de la realidad. Para evitar esta aporía he sugerido que existe simetría matemática completa: que todas las estructuras matemáticas existen también físicamente. Toda estructura matemática corresponde a un universo paralelo. Los elementos de este multiverso no residen en el mismo sitio, sino que existen fuera del espacio y el tiempo. La mayoría se encuentran vacíos de observadores.
¿Debe usted creer en universos paralelos? Hay dos argumentos principales en su contra: que son un derroche y que son extraños. El primer argumento sostiene que las teorías de multiverso son vulnerables porque toman como premisa la existencia de mundos que jamás podremos observar. ¿Por qué iba a ser la naturaleza tan derrochadora como para complacerse en la opulencia de una infinidad de mundos diferentes? Sin embargo, puede dársele la vuelta a este argumento y usarlo a favor de un multiverso.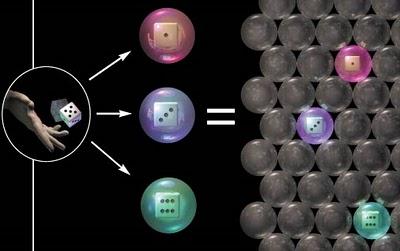
Así serían los universos paralelos en la intepretación de Everett. Infinitos universos posibles al tirar los dados.
¿Qué derrocharía la naturaleza? Ciertamente no espacio, masa o átomos; el nada polémico multiverso de Nivel I ya contiene una cantidad infinita de los tres y, por lo tanto, ¿a quién le importaría que la naturaleza derrochase un poco más? El verdadero problema se esconde en la aparente pérdida de sencillez. Al escéptico le perturba tanta información necesaria para especificar cada universo no visto.
La objeción acerca de la extrañeza es estética, no científica; sólo adquiere sentido dentro de la visión aristotélica del mundo. Y ¿qué esperábamos? Cuando planteamos una pregunta profunda sobre la naturaleza de la realidad, ¿no habremos de esperar una respuesta que parezca extraña? La evolución nos ha dotado de intuición para esa física cotidiana de la que dependía la supervivencia de nuestros remotos antepasados. Cuando nos aventuramos más allá del mundo cotidiano, deberíamos esperar algo que nos parezca estrafalario.
Nuestro juicio se reduce por tanto a qué encontramos más derrochador o inelegante: muchos mundos o muchas palabras. Tal vez nos acostumbremos gradualmente a los extraordinarios caminos de nuestro cosmos, y descubramos que su extrañeza forma parte de su encanto.
Por: Max Tegmark, profesor de física y astronomía de la universidad de Pennsylvania.
Fuente: Onironautas.org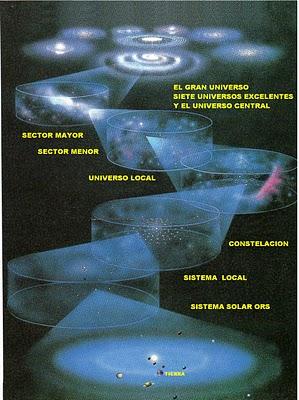
Conformación del "Gran Universo".
Quantum opina:
El último tipo de universo paralelo abre un mundo de posibilidades. Los universos pueden diferir no sólo en la ubicación, propiedades cosmológicas o estado cuántico, sino también en las leyes de la física. Existiendo fuera del espacio y el tiempo, son casi imposibles de visualizar; lo mejor que uno puede hacer es pensar en ellos en forma abstracta, como esculturas estáticas que representan la estructura matemática de las leyes físicas que los gobiernan.
En este sentido, los multiversos de más alto nivel son los más sencillos. Pasar de nuestro universo al multiverso Nivel I elimina la necesidad de especificar condiciones iniciales; pasar al de Nivel II elimina la de especificar constantes físicas, y el multiverso Nivel IV elimina la de especificar cualquier cosa. La opulencia de la complejidad reside únicamente en las percepciones subjetivas de los observadores; es decir, en la perspectiva de la rana. Desde el punto de vista del ave, el multiverso no podría ser más sencillo.
El pasado artículo es la parte final del estudio realizado por el cosmólogo Max Tegmark, profesor de física y astronomía de la universidad de Pennsylvania y publicado en la revista "Investigación y Ciencia", en julio 2003. El estudio fue presentado en 4 publicaciones sucesivas; las mismas están disponibles en nuestra página a traves de los links que detallamos más abajo. Espero les guste.

