Ecuaciones Diferenciales : Planteamiento de Problemas Parte 2

Hola Queridos Lectores estudiantes y profesores que visitan nuestro sitio de enseñanza virtual en esta ocasion continuamos con el curso de ecuaciones diferenciales donde a traves de los ejercicios planteados mostraremos procedimiento de solucion ya que es un tema interesante y que debemos llevar a un Feliz termino para que la matematicas fluya en conocimiento.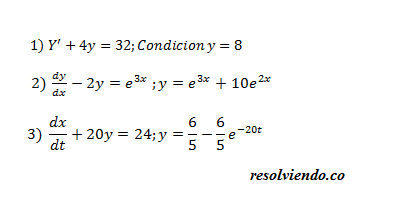

Solucion
1) Y' + 4y -32 =0
Condicion 1 ; Y=8 (1)
Resolvemos para el Valor de Y'
Y' = 32 - 4y = 32-32 =0Y' =0 (2)
Reemplazamos en la ecuación General y Se Obtiene:
0 + 4(8) - 32 =00=0 Condicion Inical Ecuacion Lineal Exacta.
2) dy/dx - 2y -e^3x =0 (*)y = e^3x + 10e^2x (1)Derivamos para calcular dy/dxdy/dx = 3e^3x + 20e^2x (2)
Reemplazamos en la Ecuacion General y Calculamos
3e^3x + 20e^2x -2(e^3x + 10e^2x) - e^3x =0Si realizamos Suma de Terminos Semejante encontramos Igualdad0=0
 3) dy/dt + 20y -24=0y = 6/5 - 6/5e^-20t (1)Derivamos la Funcion (1) para Obtener (2) dy/dt = 24e^-20t
Reemplazamos en Ecuacion General Para Encontrar Igualdad
24e^-20t  + 20(6/5 - 6/5e^-20t) -24 =0
Se verifica congruencia en la nomenclatura realizado y se Obtiene la igualdad
0=0
Con esto damos paso a la segunda PARTE de Solución de Ejercicios de Ecuaciones Diferenciales de Curso que se esta realizando por parte del Equipo de www.resolviendo.co