El reciente Premio Abel concedido a László Lovász y Avi Wigderson, y del que dimos cuenta en Matemáticas y sus fronteras, nos lleva a una reflexión sobre la relación entre la llamada matemática discreta y la teoría de computación.

Uno de los nombres claves en la computación es, sin ninguna duda, el matemático Alan Turing, quien diseñó uno de los constructos mentales más relevantes del siglo XX, la máquina de Turing. Esos algoritmos son la esencia del software que subyace en nuestros ordenadores y es una clara muestra de cómo lo discreto es esencial para la computación.
Como es bien conocido, los ordenadores trabajan con un sistema binario de numeración, con unos y ceros (1 abierto, 0 cerrado), y en cantidades discretas. Lovász es un experto en teoría de grafos (recuerdo una excelente conferencia suya sobre grafos muy grandes), y los grafos son esenciales en muchas cuestiones de la computación. Sus primeros resultados los desarrolló con el propio Paul Erdös.
En su trabajo posteror, desarrolló algoritmos para tratar de resolver problemas. Uno de sus resultados más notables fue el llamado algoritmo LLL de reducción de bases de celosía Lenstra-Lenstra-Lovász, un algoritmo en tiempo polinómico que debe su nombre a las iniciales de sus creadores Arjen Lenstra, Hendrik Lenstra y László Lovász. Este algoritmo se usa para la factorización de polinomios con coeficientes racionales, para encontrar aproximaciones racionales simultáneas a los números reales, y para resolver problemas de programación lineal. Se usa además en criptografía.
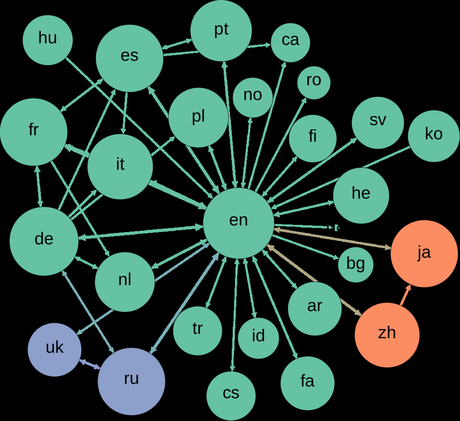
El grafo formado por los editores de Wikipedia (aristas) que contribuyen a las diferentes versiones lingüísticas de Wikipedia (vértices) durante un mes del verano de 2013
Por otra parte, Wigderson estudia los problemas computacionales para tratar de determinar la dificultad de los algoritmos para resolverlos, en lo que se conoce como teoría de la complejidad. El problema clave es en cuánto tiempo (o en cuántos pasos) el algoritmo resolvería el problema. La clase general de preguntas para las que algún algoritmo puede proporcionar una respuesta en tiempo polinómico se denomina “clase P”. Para algunas preguntas, no hay una forma conocida de encontrar una respuesta rápidamente, pero si se proporciona información que muestre cuál es la respuesta, es posible verificar la respuesta rápidamente. La clase de preguntas cuya respuesta puede verificarse en tiempo polinómico se denomina NP, que significa “tiempo polinómico no determinista”. Pues bien, uno de los siete problemas del milenio es precisamente probar si P es igual o no a NP.
Uno de los resultados más sorprendentes de Wigderson es que los problemas difíciles (hard) se pueden resolver si se usan algoritmos ales leatoriedad en los problemas computacionales. Muchos problemas difíciles pueden resolverse con mayor rapidez si se abordan con algoritmos que dependen de la aleatoriedad. Poco después fue capaz de probar que en realidad esos algoritmos se podían convertir en otros deterministas que eran tan eficaces como los aleatorios.

Solución de un problema de viajante de comercio: la línea negra muestra el bucle más corto posible que conecta cada punto rojo.
La citación del premio Abel dice que “Gracias al liderazgo de Lovász y Wigderson, la matemática discreta y el campo relativamente joven de la informática teórica se han establecido como áreas centrales de la matemática moderna”.
Las tres cuestiones que nos planteamos son las siguientes. Si tan importantes son las investigaciones en matemáticas discretas en relación con sus aplicaciones a la computación:
1. Cuál es el nivel de la investigación matemática española en combinatoria, teoría de grafos y en general en matemática discreta?
2. ¿Existen en España equipos interdisciplinares de matemáticos e informáticos que aborden estas cuestiones?
3. ¿Cuál es el impacto de estas investigaciones en la tecnología desarrollada en España?
En 2005 publicamos un estudio titulado La investigación matemática española de difusión internacional: estudio bibliométrico del período 1996-2001, elaborado por María Bordons, Isabel Gómez, María Teresa Fernández, Fernanda Morillo, David Martín de Diego y yo mismo, una colaboración con el entonces CINDOC, en el que examinamos la especialización de las matemáticas españolas en relación con Europa, Estados Unidos y el mundo, comparando la sproducciones relativas en los campos de la MSC. De ese estudio, concluíamos:
Resulta muy llamativa la alta actividad relativa de España en Análisis funcional (código46). Menos llamativo, pero también digno de resaltar es la actividad del país en Análisis de Fourier (código 42) y Teoría de juegos (código 91). Por el contrario, España muestra baja actividad relativa en algunos temas como Combinatoria (código 5), Teoría de números (código 11), Teoría de sistemas (código 93) y Mecánica de fluidos (código 76), temas a los que el mundo dedica cerca del 3% de la producción en cada caso, y en los que nuestro país muestra un IE<0,7.
Para comprobar si la situación había variado en estos últimos años, haciendo una consulta grosera en MathSciNet. Así, desde 2005 a 20020, se encuentran 1394 papers de autores españoles con la clasificación de “Combinatoria”, una media de 87 por año. La mayoría de la producción se centra en el ámbito de las universidades catalanas y andaluzas, con una más reducida presencia de la UC3M y la URJC de Madrid.
La producción, aunque parece haber aumentado (un 1,95% del total mundial), se mantiene por debajo de la de otras líneas de investigación en cuanto a cantidad que no en calidad, lo que indica que es una disciplina que precisa aumentar el número de investigadores.
En cuanto a las colaboraciones con la informática, me gustaría destacar las del grupo GAPCOMB (Geometric, Algebraic and Probabilistic Combinatorics), asentado en la Universidad Politécnica de Cataluña y apoyado por la Barcelona Graduate School of Mathematics. Pero es claro que necesitaríamos más grupos donde se produzca ese cruce de caminos entre ambas disciplinas
En cuanto al tercer tema, me temo que no soy capaz de identificar actividades en ese sentido (y agradecería recibir información sobre ellas si es que ya existen).
En conclusión, este Premio Abel nos llama la atención sobre la relevancia de la Combinatoria sino también sobre la necesidad de impulsarala más en España.
___________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).
