InterStelar: La radiación Hawking

No se si se puede considerar un homenaje a S. Hawking publicar esto cerca del aniversario de su muerte, pero en cualquier caso ya era hora de que volviese sobre las características de los agujeros negros no tratadas en la entrada anterior Las cuentas de InterStellar usando como excusa InterStellar.
Hawking descubrió este fenómeno en 1973 mientras trabajaba con el profesor Penrose. Sus resultados estaban inspirados y formaban parte de la termodinámica de los AN desarrollada entre otros por Bekenstein,  Zel'dovich y Starobinski. Aquí se establece un paralelismo entre los principios de la termodinámica y las propiedades que se conocían de los agujeros negros en rotación de tal manera que se podía asignar una temperatura a los agujeros negros. Pero claro, si la temperatura del agujero negro es superior a la del espacio que le rodea entonces ¡los agujeros negros tienen que emitir calor!
Aprovechándome de que el profesor Hawking demostró rigurosamente por dos métodos distintos la fórmula que asigna una temperatura a un agujero negro,  usaré una historia sobre el vacío y leyes básicas para alcanzarla.
En primer lugar, una onda solo puede ver, detectar e interaccionar con un objeto cuando es mayor que su longitud de onda. Por lo tanto, una onda solo podría ver el agujero negro (y ser absorbida por este) cuando la longitud de onda es menor que el tamaño de agujero negro.
Las ondas con longitud de onda λ mucho mayor que el agujero negro no serán absorbidas por él porque no lo "ven".

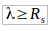
Dónde R_s es el radio de Schwarchild

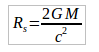
Por otro lado, según la mecánica cuántica un fotón tiene asociada una energía a su longitud de onda dada por la fórmula:
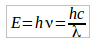h constante de Planck, ν frecuencia y c velocidad de la luz
Juntando los dos hechos anteriores, los fotones que podrían escapar (no ver)  serán los que tendrían un energía inferior a
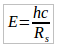Desde la física estadística nos llega la equipartición de la energía que asegura que bajo ciertas condiciones como que haya equilibrio térmico (todo el gas está a la misma temperatura) cada fotón tendrá de media una energía E = kT (en realidad sería 1/2 kT pero para cada frecuencia hay dos polarizaciones) siendo k la constante de Boltzmann.
Otro detalle proveniente de la mecánica cuántica se refiere al inefable principio de incertidumbre según el cual es imposible conocer con exactitud la energía del estado en el que esta nuestro sistema a menos que lo vigilemos continuamente. Es decir, la energía de nuestro sistema bailará alrededor de una energía (fluctuará) y estas fluctuaciones serán tanto mayores cuanto menor sea el tiempo que duren. Esto implica que hasta se podrán crear partículas de la nada si duran muy poquito tiempo. Así que nuestro vacío esta realmente repleto de fotones que aparecen y desaparecen.
Si en este vacío tenemos un agujero negro, algunas de estas partículas del vacío serán absorbidas y otras no, así que nos dará la impresión que del agujero negro (en realidad del vacío que rodea el agujero negro) vienen partículas con una energía asociada a una temperatura. Juntando las dos fórmulas anteriores sobre la energía de estos fotones:

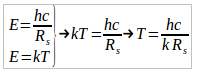
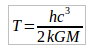
Hawking escribió dos artículos sobre este efecto, en el primero se basó en el análisis de las funciones de onda en un espacio-tiempo curvo de las partículas que interaccionan con un agujero negro, y en otro artículo (matemáticamente muy bonito) usaba una integral 4D con el cambio de variable a tiempo euclídeo (el tiempo como numero imaginarios) y comparaba el resultado con una herramienta de la mecánica estadística llamada función de partición que relaciona la distribución energética por niveles  con la temperatura de un sistema de partículas.
Permanezcan atentos a sus pantallas: la próxima entrega, la curvatura de la luz por un campo gravitatorio.