Johannes Kepler

Hasta la irrupción de Copérnico a principios del siglo XVI, la astronomía apenas había evolucionado desde la Grecia clásica. El viejo canónigo polaco inició la revolución científica al asegurar que era el Sol, y no la Tierra, el que ocupaba inmóvil el centro del universo.
Copérnico acertó en su disposición del sistema solar, pero no abrió un nuevo camino para la ciencia, sino que se pasó el resto de su vida tratando de ajustarlo en la física medieval. Como afirmaría el escritor Arthur Koestler en Los sonámbulos (1959), "era como intentar encajar un motor de turbopropulsión en una vieja y destartalada diligencia".
Entre aquellas viejas doctrinas intuidas por Pitágoras o Platón y sistematizadas por Aristóteles había quedado prendida la idea de que el movimiento de los astros era circular y uniforme. Este dogma no se rompería hasta que un matemático alemán con veleidades místicas y un talento natural para la abstracción teórica fijase sus leyes, Johannes Kepler.

Nada al azar
Kepler (1571-1630) se dio a conocer con una obra que concibió a partir de una revelación súbita del misterioso cosmos. Tenía 24 años y había abandonado sus estudios de Teología para aceptar una plaza de astrónomo y matemático en el seminario austríaco de Graz.

Kepler veía a Dios como un gran geómetra: su creación respondía a un plan prefijado de distancias y proporciones perfectas.
Conocía las tesis de Copérnico y comulgaba con el sistema heliocéntrico, pero su curiosidad traspasaba los postulados del canónigo. Creía en la armonía del mundo y veía a Dios como un gran geómetra: su creación respondía a un plan prefijado de distancias y proporciones perfectas. Nada podía haber sido fijado al azar. Por eso se preguntaba por qué había seis planetas, qué había detrás de su movimiento y por qué los separaba una distancia y no otra.
El joven Kepler quería desentrañar el plan de Dios. "Creo que fue un designio divino que recibiera por casualidad lo que antes no había podido alcanzar con ninguno de mis esfuerzos; lo creo sobre todo porque siempre había rogado a Dios que me concediera éxito en mi cometido", relató el astrónomo.
El 19 de julio de 1595, mientras enseñaba las conjunciones del zodíaco, Kepler dibujó un triángulo equilátero con un círculo inscrito y otro circunscrito. El radio de este era el doble del otro.
De repente, pensó que esas proporciones eran casi las mismas que había entre Júpiter y Saturno. Recordó que existen cinco sólidos regulares (cuerpos en los que todas sus caras son polígonos regulares iguales entre sí) susceptibles de ser inscritos en una esfera: tetraedro, hexaedro, octaedro, dodecaedro e icosaedro.
Tantos cuerpos como intervalos entre planetas. Y creyó ver en ellos la arquitectura secreta del universo. "La Tierra es la medida para el resto de las órbitas, a ella [la órbita terrestre] se circunscribe un dodecaedro; la esfera que lo comprenda será la de Marte. La órbita de Marte está circunscrita en un tetraedro; la esfera que lo comprenda será la de Júpiter. La órbita de Júpiter está circunscrita por un cubo; la esfera que lo comprenda será la de Saturno. Ahora ubica un icosaedro dentro de la órbita de la Tierra; la esfera inscrita en él será la de Venus. Sitúa un octaedro dentro de la órbita de Venus; la esfera inscrita en él será la de Mercurio. He aquí la causa del número de planetas", argumentó en El secreto del universo (1597). Basta decir que no hay seis, sino ocho planetas (el noveno, Plutón, se excluyó de la lista en 2006), para desbaratar aquel arrebato místico-científico.

Kepler envió su libro a astrónomos de la talla de Galileo y a un aristócrata danés considerado el más preciso observador de los cuerpos celestes, Tycho Brahe.
No obstante, tal como dijo Koestler, la historia de la ciencia está llena de verdades estériles y mentiras fértiles, y esta fue una de las segundas. A pesar de su errónea premisa inicial, El secreto del universo estaba repleto de valiosas intuiciones y de una idea que marcaría el rumbo del científico, la búsqueda de las leyes armónicas del cosmos.
Kepler envió el libro a astrónomos de la talla de Galileo Galilei y a un aristócrata danés considerado como el más preciso observador de los cuerpos celestes, Tycho Brahe. Galileo se limitó a responder con un correcto agradecimiento; Brahe detectó enseguida el genio del joven y le envió una carta comedidamente crítica y elogiosa junto a una invitación para que le visitara.
Kepler solo contempló la propuesta cuando la Contrarreforma y la persecución religiosa precipitaron su salida de Graz. Sin hogar ni dinero, el 1 de enero de 1600 se encaminó al castillo de Benatky, la residencia de Brahe a las afueras de Praga.

Un tándem sin igual
Tycho Brahe había llegado a Praga tras ser expulsado de la isla-observatorio de Ven por sus desavenencias con el rey danés Cristián IV. Era un hombre caótico, arrogante y de fuerte temperamento, y se hacía rodear de una camarilla de ayudantes, familiares y aduladores que se convertirían en una pesadilla para el susceptible Kepler.
En su juventud, el aristócrata había conocido mundo, aventuras y reyertas. En uno de sus famosos duelos perdió el apéndice nasal, y tuvo que sustituirlo por una pieza de oro y plata que le daba un aspecto fiero y estrafalario.
Frente al coloso danés, Kepler parecía un hombrecillo insignificante. Corto de vista, frágil de salud y de carácter retraído, el astrónomo alemán no pasaba de ser un convidado de piedra en la sucesión de banquetes, alborotos y extravagancias que se daban en Benatky.
Sin embargo, ambos encajaban científicamente como un engranaje. Kepler había desarrollado su teoría de los sólidos regulares deduciendo a priori el plan secreto del creador. Aunque todo parecía bien ensamblado, necesitaba corroborar su tesis con pruebas irrefutables.
Brahe, por su parte, poseía un tesoro de datos y mediciones, pero carecía de talento abstracto para levantar con ellos una teoría sólida. Ambos se necesitaban y complementaban más de lo que estaban dispuestos a admitir. "Sin los datos observacionales de Brahe, Kepler jamás habría encontrado sus leyes planetarias, y con ellos, nadie excepto él habría logrado ese maravilloso descubrimiento", afirma Max Caspar, el más exhaustivo biógrafo de Kepler.

Las últimas palabras de Brahe antes de morir sonaron como una súplica a Kepler: "Que no parezca que he vivido en vano".
Celoso del trabajo de toda una vida, Tycho solo compartía con Kepler datos aislados e inconexos. Un muro de vanidades y desconfianzas se levantaba entre ambos, aunque fue un estudio de la órbita de Marte encomendado por Brahe lo que permitió a Kepler alcanzar sus dos primeras leyes universales. Kepler apostó que lo resolvería en ocho días y tardó casi ocho años.

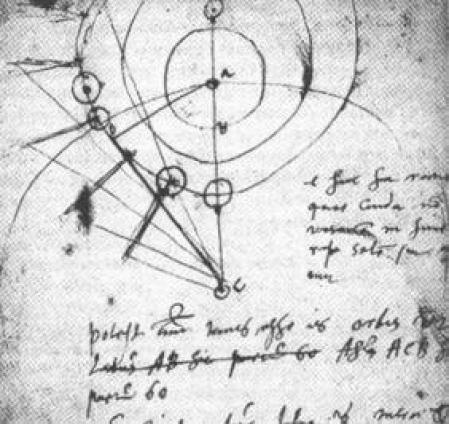
Mucho antes de lograrlo, apenas dieciocho meses después del encuentro entre ellos, Brahe murió tras uno de sus desmesurados banquetes. Sus últimas palabras sonaron como una súplica a Kepler: "Que no parezca que he vivido en vano". Johannes pudo acceder a las tablas de datos de Tycho y trabajar por fin en plenitud. Tras muchos cálculos y tanteos, creyó haber encontrado la órbita del planeta rojo.
Pero, cuando realizó las comprobaciones posteriores, valiéndose de dos mediciones raras del archivo del danés, observó que la trayectoria se desviaba en ocho minutos de arco. "Aquellos ocho minutos [...] señalaron el camino hacia la renovación de toda la astronomía", escribiría Kepler.
Por alguna extraña razón, el círculo, la más perfecta de las formas geométricas, no encajaba en la órbita de Marte. Contrariado e ilusionado a la vez, el astrónomo tuvo que despojarse de sus prejuicios para admitir que la órbita que buscaba se ajustaba a una "vulgar" figura ovalada, una elipse con el Sol en uno de sus focos. Así surgió la primera de las leyes planetarias.

Kepler invalidó el viejo axioma del movimiento circular y uniforme de los planetas y anticipó la física de Newton.

Con esos dos primeros principios, enunciados en la Nueva astronomía, Kepler invalidó el viejo axioma del movimiento circular y uniforme. Y, al situar en el Sol la causa impulsora de los astros, anticipó la física de Newton, sin llegar a definirla.
Kepler completaría su aportación a la ciencia con una tercera ley, publicada en su obra de madurez, La armonía del mundo (1619): "El cuadrado de los períodos orbitales de los planetas [el tiempo que tardan en dar una vuelta alrededor del Sol] es proporcional al cubo de sus distancias medias al Sol". El matemático buscaba una fórmula así desde su juventud, una prueba de que el cosmos estaba ordenado. Esa norma fue esencial para que Newton formulase la ley de la gravitación universal, la respuesta a la pregunta esencial de la cosmología: ¿por qué se mueven los planetas?
Kepler descubrió también que un planeta, al avanzar por su órbita, arrastra un área imaginaria en forma de cuña, que es más larga y estrecha cuanto más lejos está del Sol y más ancha y corta cuanto más cerca. Y, a pesar de esas formas distintas, el movimiento de los planetas barría áreas iguales en tiempos iguales. Así reza su segunda ley.