La importancia de ser un protón

Los átomos en los que un electrón está reemplazado por un muón (electrón muónico) se conocen como átomos muónicos. El muon es parecido al electrón en que tiene su misma carga negativa pero con una masa 200 veces superior. Con un protón y un electrón se construye el átomo más ligero que existe, el hidrogeno. Si se sustituye el electrón del átomo de hidrogeno por un muón se obtiene el hidrogeno muónico. Qué importancia tiene esta sustitución?. Pues sirve para obtener las dimensiones del protón y en consecuencia las dimensiones de todo el cosmos.

El protón puede considerarse como el ladrillo fundamental de la construcción de todo el universo. Pero muchas de sus propiedades, su tamaño y su momento magnético anómalo no están muy bien comprendidas. Para determinar el tamaño del protón, se considera como si todo su carga estuviera concentrada en una esfera de radio r_p. Y para medir este radio se ha utilizado la interacción del electrón con el protón. Hasta hace poco las medidas más precisas sobre el radio del protón están dadas por la compilación de las constantes físicas CODATA. Se basan en la aplicación de las medidas espectroscópicas del átomo de hidrogeno junto con los cálculos de la electrodinámica cuántica (QED) del estado fundamental del hidrogeno. El valor es 0,8768(69)·10^-15 m que indicamos por 0,8768(69) fm, donde fm indica fentometros, una abreviación para 10^-15 m. Vea “dimensiones atómicas”.

En 1913 Niels Bohr presentó una teoría del átomo de hidrogeno partiendo de un principio clásico pero introduciendo la característica de que el momento cinético esta cuantificado, esto quiere decir que es igual a h/2π, donde h es la constante de Planck.

Partiendo de la mecánica Newtoniana, el electrón gira en torno del protón con una velocidad v y se encuentra sometido a la fuerza de atracción eléctrica, esto determina el tamaño del átomo de hidrogeno.

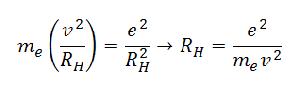
La condición cuántica sobre el momento cinético indica lo siguiente

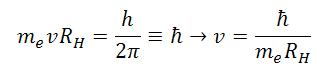
Juntando las dos ecuaciones obtenemos el radio del átomo de hidrogeno R_H

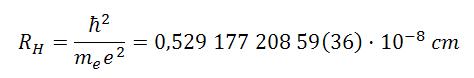
A partir de aquí Bohr fue capaz de explicar el espectro del átomo de hidrogeno, la teoría coincidía plenamente con la experiencia. La condición cuántica era extraña en la física clásica pero daba resultados. Hay que decir que esta teoría planetaria de los átomos no se debe aceptar, está muy equivocada. El hecho de que de buenos resultados en el átomo de hidrogeno es una casualidad. Esta casualidad hizo posible que Bohr se animara a continuar por este camino cuántico e impulsara a los demás a crear una teoría cuántica de los átomos.

El desarrollo de la física avanzó rápidamente a partir de estos descubrimientos hasta llegar a dos teorías matemáticas de la física cuántica: la mecánica matricial de  Werner Heisenberg en 1925 y la mecánica ondulatoria de Erwin Schrödinger en 1926. Poco más tarde el propio Schorödinger demostró que tanto la visión matricial como la ondulatoria eran una misma teoría pero vestidas con matemáticas diferentes.

Pues bien, volvamos al radio del átomo de hidrogeno, comprobaremos que es inversamente proporcional a la masa del electrón. Esta es la clave para estudiar al protón y aquí es donde entra en juego el muón (µ) que es 206 veces más masivo que el electrón. A partir de los datos de CODATA

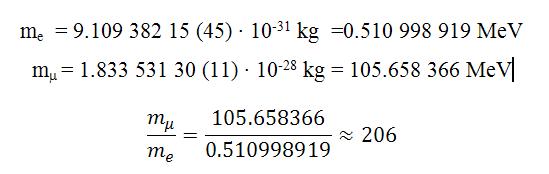
Si en lugar de observar el espectro del átomo de hidrogeno (protón + electrón) podemos observar el espectro del hidrogeno muónico (protón + muón), el radio del hidrogeno muónico será unas 206 veces menor y por tanto la interacción muón-protón será mucho mayor y más precisa. La longitud de onda también es inversamente proporcional a la masa y por tanto la longitud de onda del muón es 206 veces más pequeña que la del electrón.

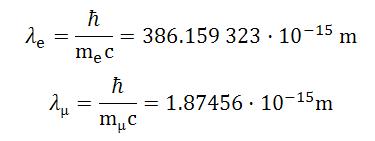
Esto significa que la función de onda del muón se superpone con la del protón (206)³ » 10⁷ veces más que la del electrón en el átomo de hidrogeno. Así pues, el muón en el hidrogeno muónico se encuentra 206 veces más cerca del protón y además las medidas son mucho más precisas que con el electrón, por tanto se pueden obtener mejores resultados sobre el tamaño del protón. Las siguientes imágenes intentan ilustrar este parágrafo.

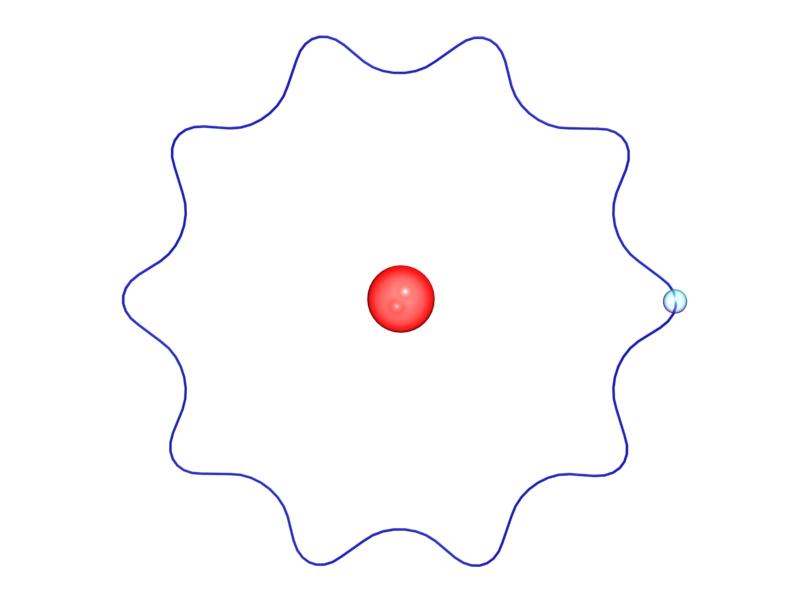
átomo de hidrogeno

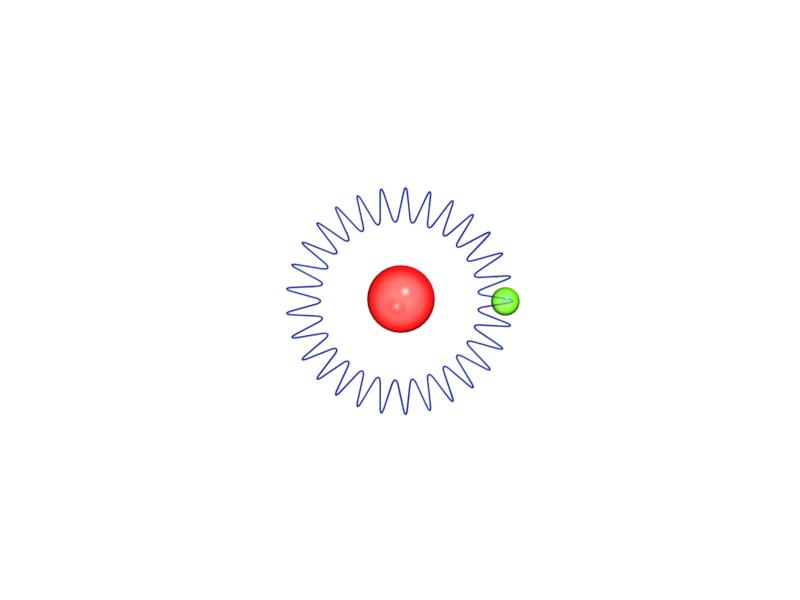
hidrógeno muonico

Este experimento lo realizo un grupo de 32 científicos presididos por Randolf Pohl en el Instituto de Óptica Cuántica Max Plank. La idea es medir el salto energético entre dos niveles cuánticos, los cálculos dan:

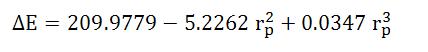
El primer término de la ecuación es debido a la polarización del vacío (vea “partículas virtuales II”), el segundo y tercer término son las contribuciones al tamaño finito del protón.

Utilizando un laser pulsante, el equipo mesuro los niveles de energía del hidrogeno muónico y los resultados experimentales dan el siguiente resultado:

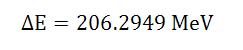
Sustituyendo en los cálculos se obtiene el siguiente valor para el radio del protón r_p = 0.84184 (36) fm. Así pues, parece que el protón es 0.00000000000003 milímetros más pequeño, cerca de un 4% menor que los últimos experimentos. La diferencia es infinitesimal, pero los protones son las partículas más comunes y junto a los neutrones forman el núcleo atómico de cada átomo del universo. Parece como un pequeño punto de carga positiva. Pero en sus entrañas es mucho más complejo, cada protón está formado por partículas fundamentales denominadas quarks, vea “átomo”.

Les explico a continuación como el protón puede considerarse el ladrillo fundamental de la construcción cósmica. No hay duda que la fuerza principal del Universo es la fuerza gravitatoria, podemos ponerla en relación con la otra fuerza fundamental, la electromagnética (vea “radioactividad”)

Para realizar la comprobación utilizamos dos protones. La fuerza de atracción gravitatoria entre dos protones es 10^-36 veces menor que la fuerza eléctrica de repulsión. Por eso en física atómica se ignoran los efectos gravitatorios. Pero la fuerza de gravedad siempre tiene el mismo signo negativo, es  de atracción. En cambio la fuerza eléctrica puede ser de atracción y repulsión, dependiendo de los signos de las cargas, positiva o negativa.  

En un cuerpo macroscópico las fuerzas de atracción y repulsión eléctricas pueden cancelarse y quedara solamente la fuerza de atracción gravitatoria, que puede llegar a ser muy importante para cuerpos masivos. Es el caso de los planetas, estrellas y cúmulos globulares.

La energía gravitacional de una partícula orbitando un objeto de masa M a una distancia r depende de M/r. Si tenemos N átomos juntos formando una esfera, la masa M de esta esfera hipotética será proporcional a N y por tanto la energía será proporcional a N/r. Puesto que es una esfera el radio será proporcional a N^1/3, recuerden que el volumen de una esfera es proporcional al cubo de su radio y el volumen es proporcional a N.

Entonces la energía es proporcional a N/N^1/3 = N^2/3 . A medida que la cantidad de átomos aumenta, la fuerza de la gravedad va aumentando. Por cada 1000 átomos la energía gravitatoria aumenta un factor 100. Así pues, tenemos que la cantidad de átomos N será proporcional a la energía gravitatoria

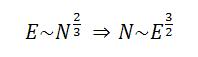
Cuando N sea mayor que

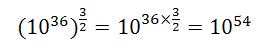
la fuerza de la gravedad será dominante. Este simple argumento nos da una idea de porque las estrellas son tan masivas. Un objeto que contiene más de 10⁵⁴ átomos de hidrogeno o protones (esto es 2·10²⁷ kg) se comprimirá por el efecto de la fuerza de atracción gravitatoria, hasta que se enciende la fusión termonuclear en su centro y esta energía compensa el colapso gravitacional. Por ejemplo, Júpiter tiene una masa de 1,899·10²⁷ kg, por poco no se convierte en una estrella.

Pero si la cantidad de protones es superior a 10⁵⁷ no hay ninguna fuerza que pueda compensar el colapso gravitatorio y se forma un agujero negro.

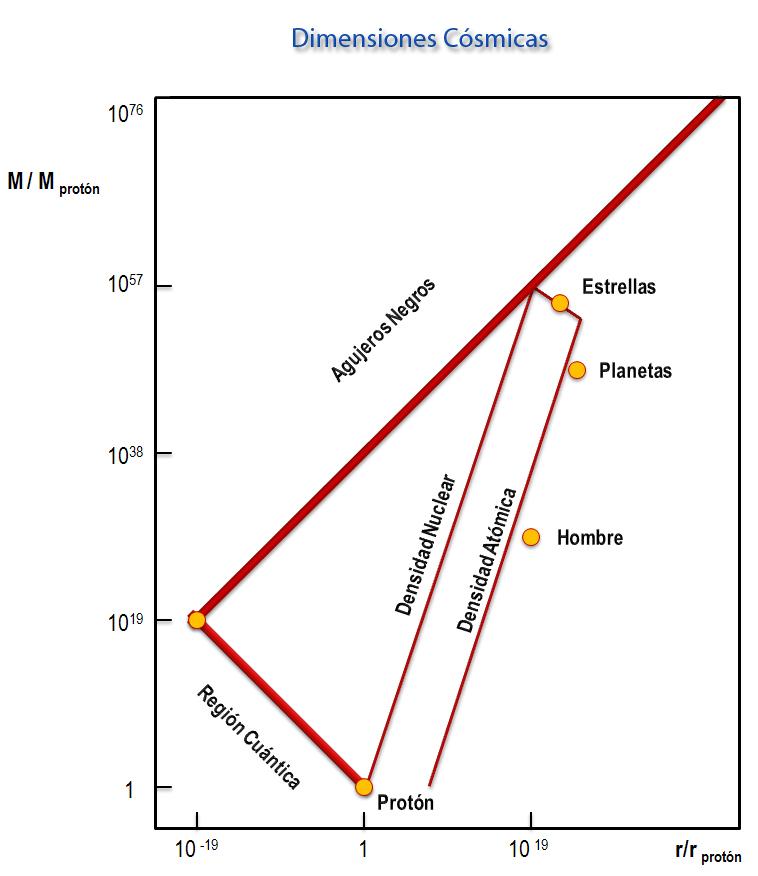
Estas y otras relaciones numéricas se muestran en el siguiente diagrama. En vertical la masa de un objeto respecto la masa del protón y en horizontal el radio del objeto respecto el radio del protón en escala logarítmica.