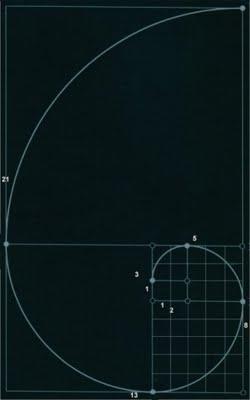
Espiral áurea.
La sucesión fue escrita por Leonardo de Pisa, matemático italiano del siglo XIII, conocido también como Fibonacci. La serie de números, tiene numerosas aplicaciones en ciencias de la computación, matemáticas, teoría de juegos y también se nos presenta en la naturaleza. La sucesión ya había sido descubierta antes por matemáticos indios tales como Pingala (200 a.c.), Gopala (antes de 1135) y Hemachandra (c. 1150), quienes habían investigado los patrones rítmicos que se formaban con sílabas o notas de uno o dos pulsos.Quizás la aplicación más conocida y por la que surge ésta solución, es al problema de la crianza de conejos. Fue descrita por el propio Fibonacci de la siguiente manera: Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y uno desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también.
La sucesión, está estrechamente relacionada con el número áureo o número de oro. Podemos ver algunos ejemplos en diversas configuraciones biológicas en los que la secuencia se presenta:
- En los modelos de crianza de conejos, como hemos visto antes, sirve para conocer el número de conejos (parejas de conejos) que habrá en 12 meses, si estos se reproducen continuamente y cada pareja de conejos produce una nueva pareja de conejos (macho y hembra). Cada conejo se puede cruzar a la edad de un mes, siendo su periodo de gestación un mes.
- En las ramas de los árboles y hojas de las plantas, se distribuyen buscando siempre recibir el máximo de luz para cada una de ellas. Por eso ninguna hoja nace justo en la vertical de la anterior, sino que lo hacen alrededor del tallo de las plantas siguiendo secuencias basadas en estos números.
- Los brazos en espiral de las galaxias y huracanes también se acomodan según los números de Fibonacci. Ver la espiral de Fibonacci para comprenderlo mejor.
- En la flora de la alcachofa, en el aloe espiral y en el romanescu (un tipo de brócoli) también se aprecia la espiral áurea.

Reproducción de conejos. | 
Aloe espiral, por atomicthumbs. |  Equinodermos. |

Brazos de una galaxia. | 
Nautilus, por lidarose. |  Alcachofas. |
- Las conchas de los Nautilus se forman siguiendo un patrón de número áureo.
- Las espirales de cualquier variedad de piña coinciden con dos términos de la sucesión de los números de Fibonacci, 8 y 13; ó 5 y 8.
- En el número de espirales en numerosas flores y frutos, que también se ajusta a parejas consecutivas de términos de esta sucesión: Los girasoles tienen 55 espirales en un sentido y 89 en el otro, o bien 89 y 144. Las margaritas presentan las semillas en forma de 21 y 34 espirales.
- Los equinodermos, un grupo de animales formados, entre otros, por los erizos de mar y las estrellas de mar, presentan morfologías que siguen patrones fractales y series de Fibonacci.
- Incluso en el ser humano y en los animales ésta proporción áurea se presenta de diferentes maneras:
- La relación entre la altura de un ser humano y la altura de su ombligo.
- La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
- La relación entre la altura de la cadera y la altura de la rodilla.
- La relación entre las divisiones vertebrales.
- La relación entre las articulaciones de las manos y los pies.
 Girasol, por Rehula. |  Sucesión en una margarita. |  Huracán Katrina y la espiral. |
 Pétalos de una rosa. |
 Romaescu por tim.G. |  Cualquier clase de piña. |
Dejando la naturaleza de lado, también se pueden apreciar estos números en el arte. Por ejemplo:
- La relación entre las partes, el techo y las columnas del Partenón, en Atenas.
- En los violines, la ubicación de las efes (los orificios en la tapa) se relaciona con el número áureo.
- El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Da Vinci, entre otros. Por ejemplo, el famoso hombre de Vitruvio.
- En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussy...
Tampoco hemos de olvidar que las series fractales, son series de Fibonacci, las cuales están muy presentes sobre todo en la naturaleza de nuestro planeta:
 Rayo, por howstuffworks. |  Nervios de la hoja, Benjamin P. |  Ríos, visto en Flickr. |
 Mar y tierra fractales en Flickr. |  Parque Natural de Doñana. |  Pavo real, por Will Brag. |
FUENTES: [1] [2] [3] [4] [5] [6]


publicado el 19 febrero a las 02:01
MMMMM no ES POSIBLE NO PUEDO ENCONTRAR NADA DE lo que buscaba jajajajaj