La vida secreta de los números. Parte II: Una historia cronológica de los números. De los naturales a los irracionales.

El presente artículo es la segunda parte de "La Vida Secreta de los Números" que fue publicado en verano de 2012 en el nº2 de la Revista Amazings (hoy Naukas).
Ir a la Parte I. 
Lo que habéis leído en la Parte I de este artículo no es la verdadera cronología de la aparición de los números. Lo que vais a leer a continuación tampoco lo será en un sentido estricto. Los diferentes conceptos numéricos han tenido muy diversos orígenes tanto en el espacio como en el tiempo. Desde un punto de vista formal, sería una historia de los números bajo la mirada de occidental (de Europa, concretamente). Y es que aunque nos sintamos el centro de la historia, al menos en matemáticas (que es de lo que yo sé, y no demasiado) resulta que hay muchas culturas con aportaciones tremendamente importantes y sin las cuales las matemáticas no podrían haberse desarrollado.
Y el hombre creó los números naturales.
Históricamente, los primeros números de los que se tienen noción son los naturales y surgen de la necesidad del hombre de contar. Pero estos números no aparecen tal y como los conocemos ahora, es decir, como todos los miembros de la sucesión 1, 2, 3, 4… sin fin. Ante las necesidades propias del hombre primitivo, tan sólo los primeros naturales son los que verdaderamente se hacen necesarios. Más allá del 7 o el 8, todo se convierte en un simple mucho.
Hoy en día se pueden encontrar tribus con costumbres primitivas y aisladas de la verdadera civilización cuyo sistema de numeración (o mejor dicho, su forma de expresar verbalmente los números) es bastante rudimentario. Así, algunos nativos del Estrecho de Torres (que separa Australia de Nueva Guinea) utilizan el vocablo urapun para representar la unidad y okosa para representar la paridad (el dos); cuando quieren decir tres no tiene más que sumar y decir okosa-urapun y si lo que les preocupa son 5 pescados, basta con decir okosa-okosa-urapun. Es muy posible que algo similar ocurriera con nuestros antepasados.
De todas formas, el hecho de que los hombres primitivos sólo tuvieran percepción de unos pocos números naturales no es nada extraño. También nos pasa a todos nosotros. Vamos a poner a prueba nuestra propia percepción de los números.
A continuación voy a mostrar un dibujo dividido en dos partes. En cada una de ellas hay una cantidad determinada de objetos (manzanas, en particular). El objetivo es el siguiente: sin contarlos, es decir, a simple vista, ¿cuántas manzanas hay en la imagen de la izquierda? ¿y en la de la derecha?

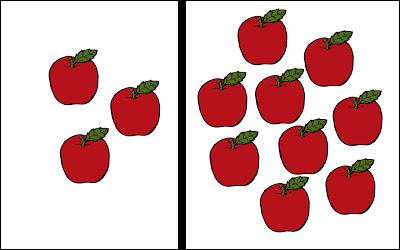
Prácticamente a todos los lectores les habrá resultado sencillo ver que eran 3 las manzanas de la imagen de la izquierda, mientras que no creo que hayáis sido muchos los que hayáis dicho que en la imagen de la derecha había 9. Y si lo habéis dicho, muchos de vosotros sois unos mentirosos por haber contado.
Pues esto mismo ocurría en la antigüedad. El hecho de que no seamos capaces de percibir visualmente las cantidades hizo necesario el surgimiento de los números: los naturales. Podríamos decir que el dedo es más poderoso que el ojo.
Poco a poco, las necesidades del hombre hicieron que se necesitara algo más elaborado que los sistemas okosa-urapun. Esta nueva contabilidad se llevaba a cabo mediante piedras: 1 por cada objeto a ser contado. El uso de piedras o calculi en el conteo, da origen etimológico a nuestro cálculo actual.

Hueso de Ishango

Y  tras la contabilidad llega la escritura numérica. Pronto se aprendió que en vez de poner piedras por cada objeto a contar, era posible hacer señales en algún otro objeto, como un hueso de animal o utilizar cuerdas con piedras (precursoras del ábaco). Uno de los más importantes ejemplos es el Hueso de Ishango (hueso de babuino con inscripciones, hallado en el área de Ishango –entre Uganda y Congo-, data del paleolítico superior y se encuentra en el Royal Belgian Institute of Natural Sciences de Bruselas). Según algunos expertos, las inscripciones van más allá de la mera contabilidad y sugieren el conocimiento de algunas operaciones aritméticas. Pero repito, esto último es sólo una hipótesis.
Con esta forma de llevar la contabilidad es claro que se impone ir agrupando los símbolos (o piedras) para no acabar con un buen montón de ellas. Así surgen los sistemas de numeración que combinan el principio aditivo (ir sumando símbolos de la unidad) con el multiplicativo, creando símbolos nuevos para grupos de 5, 10, 50, 60… unidades. Uno de los más conocidos es el clásico sistema de numeración romano (aunque con reglas más complicadas en las que también interviene, en cierto modo, la posición).

Y llegaron los racionales: fracciones babilónicas y egipcias
En cuanto las civilizaciones avanzaron, pronto surgió la necesidad de expresar numéricamente partes de un todo. No pensemos en los típicos trozos de tarta, porque dudo que a orillas del Nilo hubiese. Pensemos mejor en partes de terrenos, o cualquier otra cuestión relacionada con la agrimensura.

Ejemplo de tablilla babilonia: Plimpton 322

En los pueblos mesopotámicos, en concreto en la Babilonia de Hammurabi, ya hay constancia del uso de fracciones. En algunas tablillas de la época (estamos hablando de los años 1800 a 1600 antes de nuestra era) se puede observar cómo los babilonios disponían de un sistema de numeración posicional en base 60. Disponían de un símbolo para la unidad y otro para el 10 y mediante yuxtaposición de ellos, formaban los símbolos para los números del 1 al 59. A partir de aquí, la posición del símbolo indica su valor (clave del sistema posicional): en primera posición el símbolo significa el número que representa; en segunda (a la izquierda de la primera), significa ese valor multiplicado por $60$; en tercera, multiplicado por $60^2=3600$, etc.… Pero lo más curioso es que, según el contexto, podían tener una (o incluso varias) posición previa a la primera, es decir, a la derecha de ésta, y que representaría el número multiplicado por $60^{-1}$. Esto es, utilizaban fracciones con denominador 60 o decimales escritos en base 60. Sin embargo, se les presentaba un grave problema: no disponían de coma decimal para separar la parte entera de la decimal.

Papiro de Rhind

Además, durante casi toda su existencia carecieron de símbolo para el cero, lo que les supuso un problema añadido, ya que no podían marcar la ausencia de una posición. Para entender esto mejor, veamos un ejemplo escrito con nuestros números (y posiciones) actuales. El número 1-0-59 representa, en base 60, a $1\cdot 3600+0\cdot 60+59=3659$. Pero como los babilonios carecían del símbolo cero, lo escribirían 1-59 (a lo más dejarían un hueco mayor entre el 1 y el 59), lo que podría confundirse con el número $1\cdot 60+59=119$. El contexto, en esta cultura, era fundamental para diferenciar un número de otro. Y lo mismo podríamos hablar de la ausencia de la coma decimal. El contexto dice si el primer dígito de la izquierda es la primera posición o la posición previa.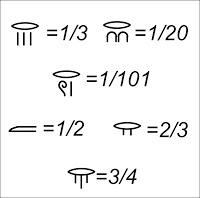

Ejemplos de fracciones egipcias.

El segundo lugar en el que aparecen las fracciones es en Egipto alrededor del año 1600 antes de nuestra era. El Papiro de Rhind es probablemente uno de los documentos matemáticos escritos más importantes de la época. Los egipcios disponían de un sistema de numeración en base 10 (curiosamente, el símbolo para 1000000 es un hombre arrodillado con los brazos levantados: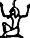 .   ¿Quién no se pondría así al ver 1000000 € hoy en día?), pero también eran capaces de escribir algunas fracciones. Las más habituales (y las que hoy se conocen como fracciones egipcias) son las de numerador 1 (1/2, 1/3, 1/4…), aunque también consideraban las fracciones 2/3, 3/4 y algunas más del tipo $\frac{n}{n+1}$. A través de sumas de este tipo de fracciones se puede expresar cualquier racional entre 0 y 1, por lo que los egipcios tenían la capacidad de trabajar con cualquier fracción. Hoy en día se puede utilizar un método basado en la llamada sucesión de Sylvester para encontrar la forma de escribir una fracción como suma de fracciones con numerador 1. Sin embargo, los egipcios, según indican algunos estudiosos de los diferentes papiros matemáticos, utilizaban otro tipo de técnicas en las que se diferenciaban los casos en que el denominador es un primo pequeño, un primo grande o un número compuesto. Pero sin duda lo más curioso de todo es que la forma de denotar estas fracciones es muy similar a la nuestra: un jeroglífico en forma de boca abierta se situaba encima del número correspondiente al denominador.
Y se perdió la razón: los números irracionales.
Acabamos de ver que los egipcios, a través de su particular forma de escribir las fracciones, podían trabajar con cualquiera de ellas. Las bases de los números racionales estaban sentadas. Estos conceptos fueron poco a poco extendiéndose hasta llegar a la cultura griega, en donde adquirieron una nueva dimensión.

Busto de Pitágoras

En la Grecia clásica, los números tenían un claro significado geométrico al ir asociados a medidas. Los números racionales, es decir, las fracciones, eran algo natural en esta cultura, pues representaban razones (cocientes) entre medidas. Pero las razones no eran cualesquiera, sino que tenían que ser exactas, es decir, del tipo 2:1, 4:3 ó 5:7.
Un grupo que se significó mucho en las cuestiones numéricas (y en otras menos científicas) fueron los integrantes de la escuela pitagórica, seguidores de Pitágoras de Samos. El lema de los pitagóricos es “todo es número”, lo que podemos interpretar como “todo era mensurable” o expresable en términos de números naturales y sus razones, los números racionales. Es a partir de este momento que la razón entre dos medidas, es decir, una medida racional, pasa a ser algo común en la cultura griega. Los racionales ya se han integrado en nuestras vidas.
Pero la gran aportación de los griegos y de los pitagóricos en particular (en torno al año 500 antes de nuestra era), es el descubrimiento de los números irracionales. La filosofía pitagórica, hemos visto, estipulaba que todo en el mundo era expresable a través de naturales o sus razones. Sin embargo la aparición del famoso Teorema de Pitágoras cambiaría esta visión del mundo.

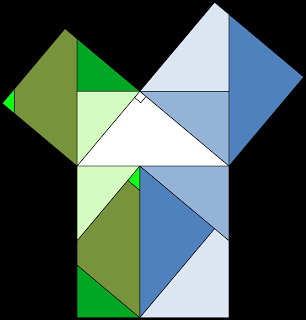
Demostración visual del Teorema de Pitágoras

El Teorema de Pitágoras establece que si tenemos un triángulo rectángulo y levantamos un cuadrado sobre cada uno de los tres lados, la suma de las áreas de los cuadrados levantados sobre los catetos (los que forman el ángulo recto) coincide con el área del cuadrado levantado sobre la hipotenusa (la diagonal). Este resultado ya aparece en algunas tablillas babilónicas como mera enumeración de ternas pitagóricas (es decir, números naturales $m$, $n$ y $p$ que cumplen $p^2=m^2+n^2$). Pero no es hasta la llegada de la matemática griega (y de la escuela pitagórica) cuando se establece como enunciado general. Pasa de ser una colección de casos particulares a ser un teorema cierto en todos los casos.
Si tomamos un cuadrado de lado 1, el Teorema de Pitágoras asegura que su diagonal es un número cuyo cuadrado es 2. Hoy en día lo conocemos como $\sqrt2$, pero en aquella época era algo bastante extraño. Durante mucho tiempo, y siguiendo su lema de “todo es mensurable” los pitagóricos trataron de encontrar una forma de expresar esta cantidad como cociente de números naturales. Todo intento resultó infructuoso. Pero tanto trabajo dejó como fruto la asombrosa conclusión de que $\sqrt2$ no es racional. Todo un terremoto intelectual.
Este descubrimiento atacaba la línea de flotación de su idea numérica del mundo, iba contra toda lógica. De ahí que comenzaran a llamar a estas cantidades alogos (sin-lógica o sin-razón, es decir, irracionales). Pero no quedó ahí la cosa. Los pitagóricos eran una suerte de secta matemática y sus descubrimientos (en particular los que atentaban contra sus ideas) no podían ser desvelados.

Espiral de Teodoro

Al parecer, uno de los miembros de la escuela, Hipaso de Metaponto, no cumplió el voto de silencio que pesaba sobre la irracionalidad de  $\sqrt2$, por lo que la hermandad pitagórica lo habría expulsado de la escuela. Cuentan las leyendas que para demostrar al mundo que Hipaso estaba muerto para los pitagóricos, se levantó una tumba con su nombre. Otras versiones afirman que los propios miembros de la hermandad pitagórica hicieron que el barco en el que Hipaso huyó de su ciudad naufragase. Pero claro, esto entra en el mundo de las leyendas. Quizás sólo fuese expulsado por meras discrepancias de carácter político y su naufragio se tratase de un terrible accidente.
De todas formas, según dice Platón en Teeteto, parece ser que Teodoro de Cirene ya habría probado también la irracionalidad de $\sqrt3$, $\sqrt5$ hasta $\sqrt{17}$. Con la llegada de Eudoxo de Cnido se estableció rigurosamente el concepto de irracional a través de una teoría general de proporciones que permitía trabajar con los inconmensurables.
Bastante después, el matemático egipcio Abu Kamil (entre el año 850 y el 930 de nuestra era) se considera que fue el primero en aceptar los números irracionales como soluciones de ecuaciones de segundo grado o como coeficientes en una de ellas, normalmente en forma de raíces cuadradas, cúbicas o cuartas. En el siglo X la matemática árabe proporciona ya pruebas generales (en lugar de las demostraciones geométricas) de la irracionalidad de ciertos números. Todos estos conceptos fueron llegando a Europa a través de las traducciones latinas del siglo XII.
Ir a la Parte I.  Continúa leyendo la tercera parte de esta entrada en este mismo blog.
Tito Eliatron Dixit
PD: Esta entrada participa en la Edición 8.5 del Carnaval de Matemáticas cuyo anfitrión es, en esta ocasión, Santi García desde Raíz de 2.  
 
Esta entrada se ha publicado originalmente en Tito Eliatron Dixit.
Si la estás viendo en otra web, probablemente estés siendo víctima de un engaño.
 
SI no ves las fórmulas correctamente, entra en Tito Eliatron Dixit, donde sí podrás verlas.