Progreso científico y aproximación a la verdad (4)

La serie de entradas sobre el concepto de verosimilitud llega a su fase "culminante", en la que expondré la concepción que he venido desarrollando. Recapacitemos algunas cuestiones importantes, que nuestro enfoque tendrá que tener en cuenta inevitablemente:
.
1) la noción de semejanza es relativamente subjetiva: dos cosas pueden ser parecidas para un sujeto, o desde cierto punto de vista, o en función de ciertos intereses, pero no ser tan parecidas en otros casos;
.
2) pese a ello, pretendemos identificar algún concepto razonable de "aproximación a la verdad" según el cual  tenga sentido la afirmación de que el objetivo de la ciencia es aproximarnos a la verdad; y
.
3) este concepto debería poder ponerse en conexión con las normas y criterios metodológicos usados por los científicos, de tal modo que podamos explicar que la razón por la que se siguen aquellas normas es porque haciéndolo así es de esperar que consigamos teorías que estén más próximas a la verdad que siguiendo otras normas.
.
Pues bien, mi sugerencia es hacer la suposición de que el grado (subjetivo) de semejanza entre dos proposiciones, A y B, depende principalmente de tres factores:
.
a) la coherencia entre A y B, que puede ser medida con la fórmula p(A&B)/p(AvB) = p(A&B,AvB); o sea, la probabilidad que el sujeto atribuye a la posibilidad de que A y B sean verdaderas las dos, dividida por la probabilidad de que sea verdadera alguna de las dos (lo cual equivale a la probabilidad de que las dos sean verdadera condicionada a que al menos una de ellas lo es); gráficamente esto corresponde al área comprendida en la intersección de los conjuntos de mundos que corresponden a ambas teorías, dividida por el área de la unión de ambos conjuntos;
.
b) al factor anterior, que considero el principal, añadimos otros dos; en primer lugar, tanto A como B pueden "emborronarse", en el sentido de sustituir B (p.ej.) por la proposición B(d), que afirma que "el mundo verdadero está a una distancia menor que d de algún mundo permitido por B"; es decir, consideramos que B no nos da una descripción "exacta" del mundo, sino "aproximada" (con grado de aproximación igual a d; recordar la entrada número 2 de la serie); una vez hecho esto, aplicamos la noción definida en el párrafo anterior, pero en vez de entre A y B, lo hacemos entre A y B(d); esto nos sugeriría definir la semejanza entre A y B como igual a p(A&B(d)/AvB(d)), eligiendo d de tal manera que el valor de esa fracción sea el máximo posible.
.
c) por último, también podemos tener en cuenta que los enunciados A o B pueden consistir en la conjunción de varios enunciados que, por las razones que sean, consideremos proposiciones independientes entre sí y relevantes para juzgar la semejanza entre las primeras; si, p.ej., B es la conjunción de varios enunciados, B1, B2, ..., Bn, podemos considerar que la semejanza entre A y B equivale al resultado de aplicar la medida de semejanza basada en la coherencia a alguna de las combinaciones de los enunciados B1, ..., Bn, en concreto, a aquella combinación cuya coherencia con A sea mayor.
.
Los criterios b y c permiten establecer que dos enunciados A y B pueden ser semejantes incluso aunque sean lógicamente contradictorios entre sí (y por lo tanto, p(A&B) sea igual a 0): si A es incompatible con B, pero no es incompatible con B(d), o no es incompatible con muchos de los enunciados Bi cuya conjunción forma B, entonces es posible que A nos parezca pese a todo bastante semejante a B. También es importante señalar que los criterios b y c pueden aplicarse a la vez: A puede parecernos semejante a B por ser coherente con algunos Bi expresados éstos en versión no exacta sino aproximada (Bi(d)).
.
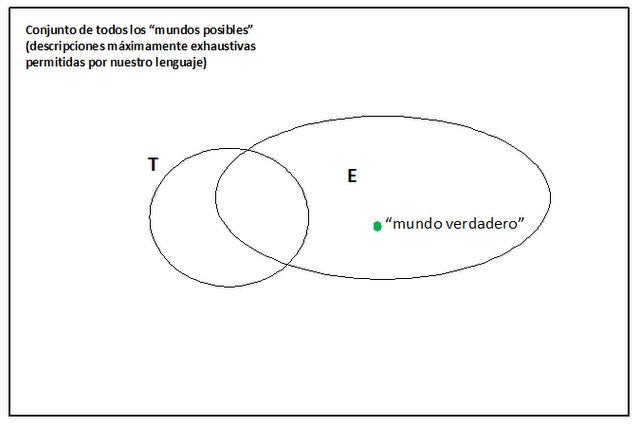Teniendo esto en mente, ¿cómo podríamos definir el "grado de aproximación a la verdad" de una teoría T? Si V representa la verdad más completa que podemos expresar con el lenguaje del que disponemos (o sea, la proposición que describe el "mundo verdadero" de la figura), una posibilidad sería p(T&V(d))/p(TvV(d)) (con la distancia d para la que esto es máximo). Otra posibilidad sería considerar a qué conjunción de proposiciones equivale V y aplicar el criterio c. La solución que me parece más prometedora es utilizar, para la determinación del grado en el que nos parece que T se ha aproximado a la verdad, la proposición que nos dice, precisamente, qué es lo que sabemos sobre la verdad: nuestros "datos empíricos" E, que generalmente consistirán en la conjunción de aquellas regularidades empíricas que las teorías deben "explicar". Mi definición favorita es, por tanto, la siguiente:
.
Vs(T,E) = Semejanza entre T y E * Semejanza entre E y V. . Es decir, la verosimilitud de una teoría T, a la luz de los datos empíricos que poseemos, vendrá dada por la semejanza que hay entre la teoría T y los datos E, ponderada por la semejanza que hay entre E y la "verdad completa", V (pues, cuanto más próxima esté E a V, más verosímil nos parecerá una teoría que sea coherente con esos datos).
.
Puesto que, por definición, estamos suponiendo que los datos empíricos son verdaderos (son los que aceptamos como verdadero sobre la verdad), entonces la definición se reduce a lo siguiente:
.
Vs(T,E) = [p(T&E)/p(TvE)][p(T&E)/p(TvE)] . = [p(T&E)/p(TvE)][p(V)/p(E)] . = [p(T&E)/p(E)][p(V)/p(TvE)] . = [p(T,E)/p(TvE)]p(V) .
Puesto que la probabilidad de V es una constante (será siempre la misma, sean cuales sean T y E), y puesto que lo que queremos es una función que nos sirva para comparar la verosimilitud de dos teorías frente a los mismos datos, o de una teoría frente a un conjunto cambiante de datos, etc., podemos suprimir la referencia a p(V) (que aparecerá en todas las comparaciones del tipo Vs(T,E) > Vs(T',E') a los dos lados de la comparación, y podremos borrarla en los dos lados), y la definición se nos queda asín:
.
Vs(T,E) = p(T,E)/p(TvE). .
A esa definición le podremos aplicar posteriormente los criterios b y c cuando sea menester.
.
En la próxima entrada empezaré a comentar las (fantásticas) propiedades de esta función.
.

Enrólate en el Otto Neurath