
El Instituto de Ciencias Matemáticas (ICMAT) participa por primera vez en la Noche de los Investigadores dentro de ‘Abre tu mente con la UAM’, el programa la Universidad Autónoma de Madrid para 2012. Para quien todavía no la conozca, el principal objetivo de esta actividad divulgativa que se celebra en toda Europa desde 2005, es “acercar los investigadores a los ciudadanos para que conozcan su trabajo, los beneficios que aportan a la sociedad y su repercusión en la vida cotidiana, en un marco festivo y lúdico, cuyos protagonistas son tanto los ciudadanos como los investigadores”.
Aprovechando el contexto del el Año Internacional de la Neurociencia, los investigadores del ICMAT hablarán del trabajo de los matemáticos en el estudio de las redes neuronales, a través de la modelización con grafos. Juanjo Rué, Ana Zumalacárregui y Carlos Vinuesa introducirán algunos conceptos de la Teoría de Grafos y de sus aplicaciones en investigaciones multidisciplinares, en particular, de las llamadas redes de pequeño mundo . El taller ‘ser simple es complicado: grafos y redes complejas’ tendrá lugar el 28 de septiembre en La Corrala (c/ Carlos Arniches 3-5, 28005) el centro Cultural de la UAM, en diversos pases desde las 18:00 hasta las 22:30.
Juanjo Rué y Ana Zumalacárregui presentan el tema de la conferencia a través el siguiente texto.
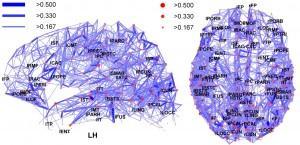
Los grafos que nos ocupan son aquellos que se usan en el modelizado de redes neuronales: los llamados grafos Small World o ‘de pequeño mundo’.
Los grafos pequeño mundo son un tipo especial donde cohabitan propiedades tanto del mundo ordenado como del completamente aleatorio. Este concepto fue introducido en el año 1998 por los investigadores Duncan Watts y Steven Strogatz en su artículo en la revista Nature titulado Collective dynamics of ‘small-world’ networks.
Este tipo de redes tienen simultáneamente las propiedades de alta conectividad en vértices cercanos (grafos regulares) y distancia pequeña entre vértices alejados (grafos aleatorios), lo que permite una alta eficiencia en el flujo de información.
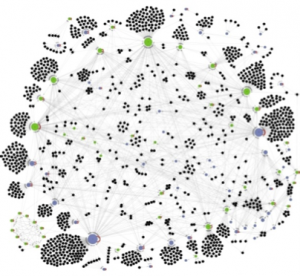
Red de regulación genética de la bacteria Mycobacterium tuberulosis. Cada vértice representa un un gen. Extraído de la web.
El mundo pequeño en parámetros
Para definir su modelo, Watts y Strogatz definieron dos parámetros: el coeficiente de agrupamiento (clustering coefficient), que indica cómo de ‘acumulados’ están los nodos de la red, y la distancia media entre vértices, que cuantifica, en media, la distancia entre dos vértices cualesquiera.
Utilizando estos conceptos, propusieron un modelo de redes de pequeño mundo cuyas características más sobresalientes son:
- Un trayecto mínimo promedio entre vértices pequeño: es decir que cualesquiera dos vértices de la red se comunican por un camino de vértices intermedios relativamente pequeño.
- Un coeficiente de agrupamiento medio elevado: si dos vértices o nodos no están conectados directamente entre sí, entonces existe una gran probabilidad de que se conecten mediante la intervención de otros nodos.
La primera descripción del modelo de Watts y Strogatz mostró que había una graduación entre lo que se puede denominar un mundo grande (un grafo regular) y un grafo aleatorio (conexiones desordenadas entre los vértices); entre estos dos extremos se hallaban las redes demundo pequeño . Se han encontrado ejemplos de redes de pequeño mundo en numerosas redes presentes en la naturaleza, desde la que define las proteínas que interaccionan en el metabolismo de las bacterias hasta las redes neuronales.
En las últimas décadas se ha observado que la estructura de muchas redes reales (redes sociales, tráfico aéreo, redes neuronales, …) se pueden clasificar de manera efectiva usando los parámetros introducidos por Watts y Strogatz en su estudio.
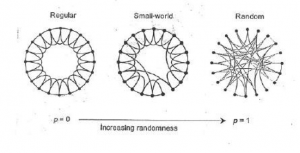
A medio camino entre los grafos aleatorios y los totalmente ordenados se hallan los grafos pequeño mundo (Del articulo original de Watts y Strogatz).
El mundo es un pañuelo
Este modelo de pequeño mundo efectivamente da una primera aproximación al problema de las redes neuronales, pero además modela con bastante fidelidad la estructura social de distintas comunidades (reales o virtuales). Y no sólo eso, sino que permite entender y explicar cómo se relacionan las personas. Más concretamente, las redes de mundo pequeño permiten ratificar la máxima de que el mundo es un pañuelo.
De hecho, la noción de pequeño mundo fue acuñada en los años 1960 por el psicólogo Stanley Milgram. Mediante un experimento conjeturó el hoy ya célebre teorema de 6 grados de separación. El experimento consistía en escoger de manera aleatoria a dos personas, una de Omaha (Nebraska) y otra de Boston (Massachusetts). A la primera le entregaba una carta que tenía que hacer llegar al segundo individuo, siguiendo una cadena de conocidos intermedios.
Los remitentes sabían el nombre del destinatario, su ocupación y la localización aproximada. Recibían instrucciones de mandar el paquete un conocido suyo que fuera el que más probabilidades tendría, de todos sus amigos, de conocer directamente al destinatario. Esta persona tendría que hacer lo mismo y así sucesivamente hasta que el paquete fuera entregado a su destinatario final.
Pese a que los participantes habitaban en dos lugares lejanos de EE UU la entrega de cada paquete solamente llevó, como promedio, entre cinco y siete intermediarios. Los descubrimientos de Milgram fueron publicados en “Psychology Today” e inspiraron la teoría de los “seis grados de separación”, es decir, la formalización de la expresión coloquial “’¡el mundo es un pañuelo!”.
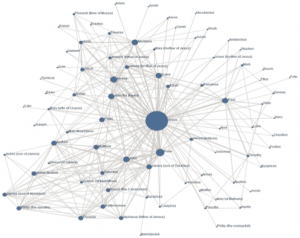
Red social del Nuevo Testamento. Cada vértice representa un personaje bíblico . Extraído de la web.
“Ser simple es complicado”, por Ana Zumalacárregui, Juanjo Rué y Carlos Vinuesa (ICMAT), es una actividad de investigadores de ICMAT englobada en el programa de la UAM para la Noche de los investigadores de la Comunidad de Madrid.
La Noche de los Investigadores Madrid 2011 es un proyecto de divulgación científica promovido por la Consejería de Educación y Empleo y coordinado por la Fundación madri+d. La Noche de los Investigadores cuenta con el apoyo de la Fundación Española para la Ciencia y la Tecnología (FECYT) y se asocia a la celebración europea de este evento que tiene lugar simultáneamente en más de 200 ciudades desde 2005.
La noche de los Investigadores en La Corrala se iniciará a las 18:00 h. hasta las 22:30 h. con múltiples actividades interactivas que se celebrarán simultáneamente en cubículos dispuestos alrededor del patio central, los asistentes podrán distribuirse entre los diferentes espacios reservados para la conversación con los investigadores.
La corrala está en la calle Carlos Arniches 3-5, en el barrio madrileño de Lavapiés
–
Ana Zumalacárregui y Juanjo Rué son investigadores del ICMAT.
Más información:
Nota de prensa del ICMAT.
En la web de ICMAT
En la web de la UAM.
La Noche de los Investigadores de la Comunidad de Madrid.
Researchers Night
