Solución cubo de Rubik 4x4_Primera parte

Actualización 28 de septiembre: He recibido un par de correos privados solicitándome el método en un único archivo (lo cual me honra bastante, dicho sea de paso). Ahora mismo, lo único que tengo son las imágenes en .jpg publicadas (que son de elaboración propia y casi artesanal), ya que el texto lo fui escribiendo sobre la marcha mientras redactaba los post, así que me pondré manos a la obra para hacer un documento que se pueda descargar al disco duro, imprimir, y tener sobre la mesa para consultar de un vistazo...
Así que, si alguien más está interesado, que me lo haga saber y se lo enviaré gustoso en cuanto lo tenga terminado.

Hace menos de un mes publiqué una entrada con un método para solucionar el cubo de Rubik 4x4, también conocido como Rubik's Revenge o Master Cube, y desde entonces no he parado de darle vueltas a la cabeza pensando si hice bien. Porque, aunque en el post advertía que no era el método empleado por los "speed-cubers", desde el primer día se destacó como una entrada con muchas visitas (la mayoría llegadas desde google), y de hecho, es la más visitada en lo que llevamos de mes... Así que más de uno estará practicando este método y, lamento decir, adquiriendo un mal hábito, porque intentar resolver el cubo con unos tiempos "decentes" no es posible con aquellos algoritmos, y cambiar luego el chip y aprender otro método supone doble trabajo (y lo digo por experiencia...).
Así que, para solucionar mi conflicto,y también un poco como penitencia por llevar a más de uno por el mal camino, he aprovechado durante un par de semanas que he estado sin conexión a Internet, y me he puesto manos a la obra. A partir de varios documentos en inglés y algún algoritmo extraído de la página de Rubikaz, preparé las imágenes que podéis encontrar en este post, y que corresponden a un método más... no sé cómo calificarlo... correcto. Y si os animáis a probarlo, descubriréis que presenta algunas ventajas sobre el antiguo. Una de ellas es la rapidez con la que el cubo puede resolverse. Otra, importantísima, es la cantidad de algoritmos que hay que memorizar, bastante menor con este método.
Así que, sin más demora, comenzamos. Como siempre, sin prisas y con mucho detalle en las explicaciones. Incluso a veces os parecerá que con demasiado detalle, sobre todo a los que ya tengáis conocimientos previos o sepáis resolver el cubo hasta un punto y vengáis buscando algún algoritmo concreto para solucionar un problema determinado... Así que a todos vosotros, paciencia. Y como siempre, para ver las imágenes con más nitidez, clicad sobre ellas.
El propósito de este método es convertir el cubo 4x4 en una especie de gran cubo 3x3, para así resolverlo con sus algoritmos, los cuales, se supone, ya dominamos. La siguiente imagen resume bien la idea general del método:

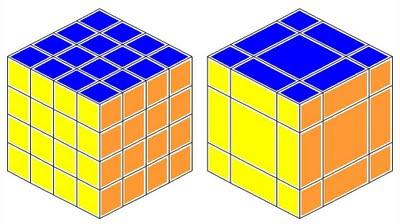
Estos son los pasos generales que seguiremos:

1. Resolver los centros de todas las caras.
2. Emparejar las aristas.
3. Aplicar algoritmos cubo 3x3.
4. Solucionar paridades (casos que no se dan en el cubo 3x3).

0.- Notación.
Estos son los nombres de las capas y el convenio de giros que vamos a emplear. A diferencia del cubo 3x3, en el cubo 4x4 sí es preciso nombrar las capas interiores de alguna forma. Mi propuesta es identificarlas con la letra minúscula de la capa adyacente, como podéis ver en la imagen:
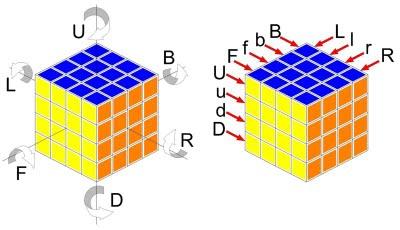Al igual que en anterior post, bajo estas líneas tenéis una lista con la definición de algunos términos empleados. Es importante conocerla para saber en todo momento a qué me refiero exactamente cuando explico el objetivo de algún algoritmo, y conocer las diferencias entre, por ejemplo, mover una pieza, girar una capa, colocar una arista...

• Cubo: así denominaremos al cubo en su conjunto.
• Piezas: son los "cubitos" que forman el cubo. Pueden ser de tres tipos: centros, aristas o esquinas.
• Cara: cualquiera de los seis lados que forman el cubo, cada uno de un color.
• Capa: además de las seis caras, las "rodajas" horizontales o verticales intermedias. En la imagen de la "notación de giros", son las indicadas con letras minúsculas.
• Girar una cara/capa: girar 90º la cara o la capa a la que se refiere.
• Girar una pieza: se refiere a cambiar la orientación de una pieza, pero sin cambiar la posición en que se encuentra.
• Colocar una pieza: se refiere a cambiar la posición de la pieza.
• Pieza invertida: llamaremos así a las piezas bien colocadas, pero mal orientadas.
• Algoritmo: fórmula compuesta de varios giros distintos, para conseguir girar o colocar correctamente una o varias piezas.

También es importante la siguiente lista para comprender los algoritmos y saber qué capa debemos mover, en qué sentido, y cuántos grados:

• Los giros serán de 90º (un cuarto de vuelta).
• X = giro en el sentido de las agujas del reloj.
• X' = giro en el sentido contrario a las agujas del reloj.
• X² = giro de 180º (media vuelta).
• (XY)ⁿ = repetir el grupo entre paréntesis "n" veces.
• Las aristas se nombrarán así: ^FL, ^BU, ^LB...
• La notación de lass esquinas será: ^UFR, ^BLU, ^DLF...
  

Con estas premisas y la notación de las caras de la imagen anterior, estos son los ejemplos de todos los giros con los que nos encontraremos:

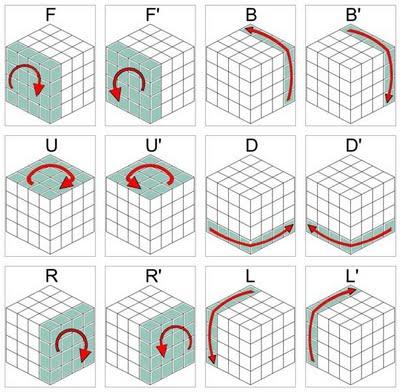
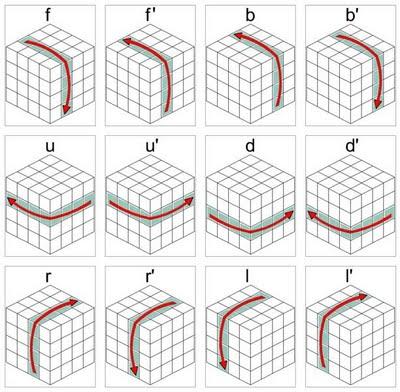
1.- Resolver los centros de las caras.
Reconozco que la primera vez que me puse por mi cuenta a resolver los centros de las seis caras, sin ayuda de ningún método, no fui capaz. Cuando intentaba solucionar el cuarto, se deshacía el tercero. Si llegaba a tener cuatro centros colocados correctamente, no veía la forma de abordar los que me faltaban sin que se desmontara alguno de los anteriores... ¡Cuánto hubiera pagado en esos momentos por tener las siguientes imágenes!
El camino que, personalmente, os aconsejo seguir, es este:

1. Resolver un centro (cualquiera) y su opuesto.
2. Resolver un centro lateral y su opuesto.
3. Resolver el último centro. Su opuesto, inevitablemente, se solucionará a la vez.

En las dos siguientes imágenes encontraréis todas las posibilidades que se os pueden presentar cuando afrontéis el primer paso (resolver un centro y su opuesto), para que no haya posibilidad de quedarse atrancado, que en estas etapas es muy habitual rendirse con la primera dificultad que se presenta, y que el cubo acabe abandonado en un cajón... A la izquierda, la posición inicial. En el centro el algoritmo. Y a la derecha, la posición final, el resultado de haber girado en el sentido correcto y en el orden adecuado cada capa.

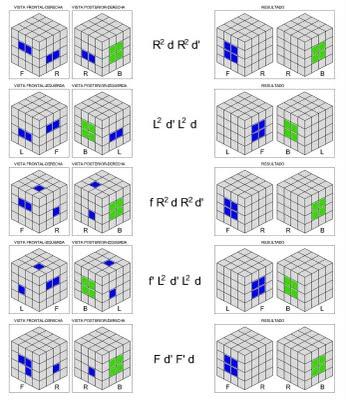
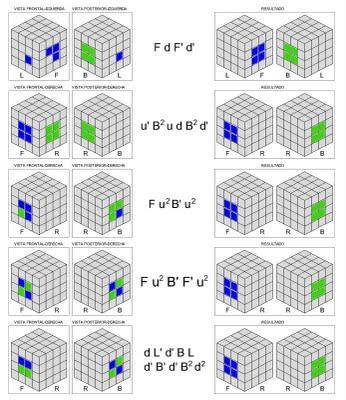
A continuación vamos a resolver un centro lateral y su opuesto, evidentemente, sin que se deshagan los dos centros que ya tendremos solucionados. De nuevo, confío no haberme olvidado de ninguna, os he dibujado todas las posiciones posibles de partida que podéis encontraros:
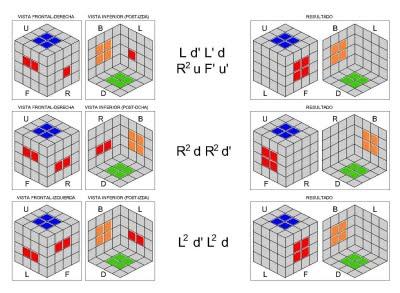
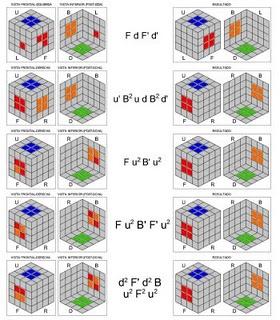Por último, con cuatro centros de cara correctamente resueltos, afrontamos los dos últimos, y tendremos que tener cuidado, ya que según la posición de los centros de cara que ya hayamos resuelto, los dos últimos no podrán colocarse indistintamente. Obligatoriamente, uno de ellos deberá situarse "a la izquierda" y el otro "a la derecha" de los que ya tenemos. La siguiente imagen clarifica bastante todo lo anterior: imaginad que ya tenemos resuelto el centro de la cara azul y de su opuesta verde, el centro de la cara roja y de su opuesta naranja. Deberemos colocar el centro blanco en la cara F y el amarillo en la cara B, nunca al contrario.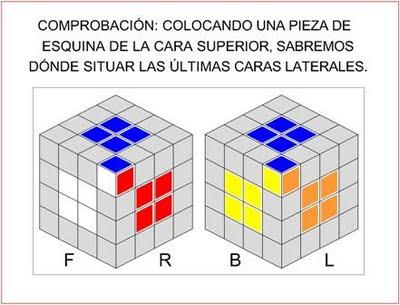

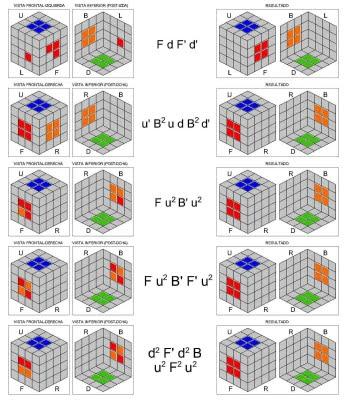
En este punto, las combinaciones que pueden presentarse ya son muchas menos. Para no perder las buenas costumbres, están todas dibujadas.
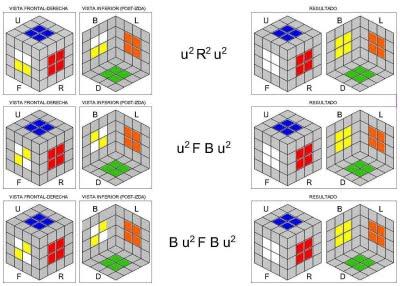
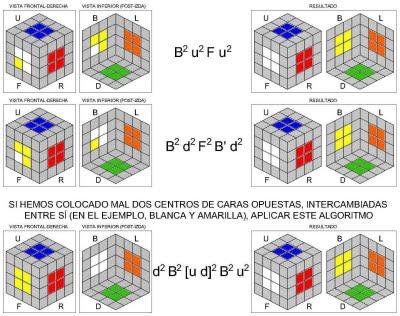Bueno, finalizo aquí este post, que está resultando demasiado extenso. En la segunda parte encontraréis los algoritmos con los que aprender aemparejar aristas y a solucionar las paridades, ya sabéis, esos casos particulares que no se dan nunca en el cubo 3x3, pero que sí se presentan frecuentemente en el cubo 4x4. Tened en cuenta que, estadísticamente, sólo en un caso de cada cuatro podremos resolver el cubo sin encontrarnos con alguna paridad. Así que tienen su importancia.
Por cierto, que no se olvide: en Rubikaz encontraréis un método que guarda bastantes similitudes con este (algunos algoritmos están sacados de allí). Pero sus ejemplos están animados, de una calidad impresionante!!! Yo me he limitado a elaborar estas humildes imágenes en .jpg, pero debéis mirarlas por el lado positivo: pueden imprimirse y dejarse sobre la mesa como apoyo mientras resuelves el cubo, sin la necesidad de estar frente al monitor... Si el que no se consuela...
Fuentes: wikipedia, rubikaz y microsiervos.