El problema que propuse decía así:
“En la siguiente imagen se muestra un sistema de engranajes compuesto, formado por cuatro ruedas dentadas.
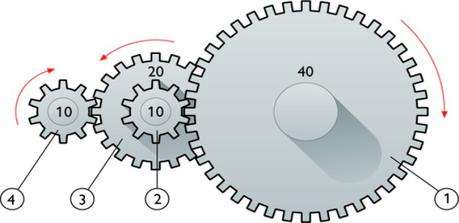
Si el número que aparece en cada una de las ruedas indica la cantidad de dientes que tiene ¿cuántas vueltas deberá dar la rueda 1 para que la rueda 4 dé 20 vueltas?”
Vamos a ver la SOLUCIÓN.
Se nos pide averiguar el número de vueltas que debe dar la rueda 1 (la más grande) para que la rueda 4 dé veinte vueltas.
Llamemos
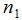
Para resolver este problema podemos intentar plantear una ecuación, donde la incógnita sea
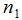
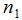
Lo vamos a hacer paso a paso, es decir, siguiendo el sistema de engranajes, empezando por la rueda 1 y terminando por la 4, observando la relación que hay entre el número de vueltas de la rueda 1 y la 2, entre la rueda 2 y la 3 y, por último, entre la rueda 3 y la 4.
Antes de empezar con el caso concreto que nos ocupa, vamos a ver la relación que se puede establecer entre dos ruedas dentadas de un engranaje. Por cierto, la rueda mayor en un engranaje de dos ruedas se denomina corona y la menor piñón.

Animación de un engranaje de dos ruedas dentadas. Imagen de dominio público.
Si nos fijamos en la animación, el piñón (la rueda pequeña) gira a mayor velocidad que la corona (la rueda grande), o lo que es lo mismo, el número de vueltas de cada una de las ruedas es inversamente proporcional al número de dientes que tiene (a mayor número de dientes menos vueltas, y viceversa).
Así, se puede relacionar el número de vueltas y el número de dientes de las dos ruedas por medio de la siguiente expresión:
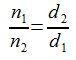
o, expresado de otra manera:
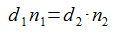
donde:
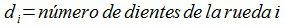
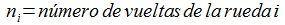
Esto es una forma de verlo, aunque quizás sea más intuitivo obtener diréctamente esta última expresión, razonando que el número de dientes de cada una de las ruedas que pasa por el punto de contacto entre ellas debe ser el mismo (a cada diente de una de las ruedas le sigue inmediatamente un diente de la otra rueda).
Fijémonos ahora en las dos primeras ruedas.
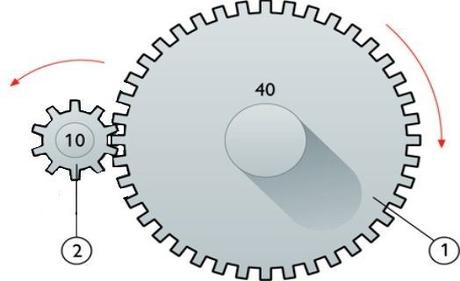
Si utilizamos la expresión que hemos visto antes, tenemos:
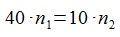
y operando, obtenemos el número de vueltas de la rueda 2 en función del número de vueltas de la rueda 1:
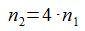
Ahora vamos a ver la relación entra las ruedas 2 y 3.
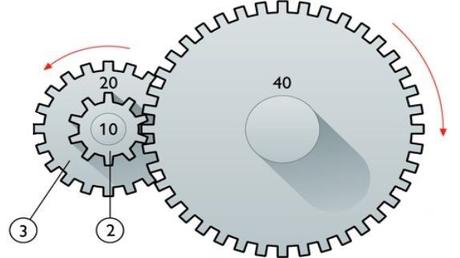
En este caso ambas ruedas tienen el mismo eje y se mueven solidarias (no se trata de un engranaje como tal), por lo que la relación que hay entre ellas es que el número de vueltas de ambas es el mismo:
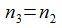
y, por lo tanto:
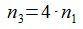
Por último, vemos qué relación hay entre las ruedas 3 y 4.
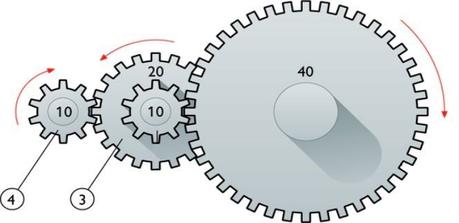
Como se trata de un engranaje formado por dos ruedas dentadas, aplicamos de nuevo la expresión que hemos visto que las relaciona, obteniendo:
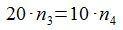
y operando:
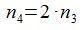
Ahora, sustituyendo
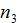
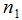
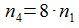
o, lo que eslo mismo:
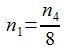
¡Pues ya lo tenemos prácticamente!
Tan solo nos queda sustituir
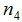
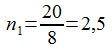
Pues ésta es la solución a nuestro problema: la rueda 1 tiene que dar dos vueltas y media para que la rueda 4 dé veinte vueltas.

