¿Subir escaleras envejece?

Me comenta mi amigo Alejandro, que en un artículo de Science se comenta que según Einstein subir escaleras envejece. Le contesto que esto tiene que ser algo relacionado con el efecto Mössbauer. Intento convencer a Alejandro en este post que subir escaleras ni envejece ni rejuvenece, pero que mire por donde pisa. Referencias: relatividad, paradoja gemelos, dilatación temporal, desplazamiento al rojo, fotón…

El artículo es “Optical Clocks and Relativity” de C.W. Chou, Science 329, 1630 (2010). Hace referencia a la teoría de la relatividad, esta teoria predice que los relojes de dos observadores en movimiento relativo o a distinto potencial gravitatorio marcaran un tiempo distinto. Es lo que se denomina la dilatación temporal. Estas predicciones de la relatividad ya habían sido observadas utilizando relojes atómicos en aviones a altas velocidades y grandes cambios en elevación.

C.W.Chou, D.B.Hume, T.Rosenband y D.J.Wineland comparando dos relojes atómicos separados una altura de 1 metro, han sido capaces de observar una dilatación temporal.

El experimento está muy relacionado con la paradoja de los mellizos. Otra consecuencia de la teoría de Einstein es que el tic-tac de los relojes es más lento cerca de objetos muy masivos, como consecuencia de la fuerza de la gravedad. En nuestra vida cuotidiana las velocidades y las alturas son tan pequeñas que los efectos relativistas no se pueden apreciar. Por ejemplo, si dos relojes idénticos se separaran una altura de 1 kilometro cerca de la superficie de la Tierra, el reloj más elevado se adelantaría tres segundos al cabo de un millón de años. Que son unas 8 mil millonésimas de segundo al día.

Esto es lo que me decía Alejandro, al subir una escalera notaremos que todo nuestro organismo funciona a un ritmo más rápido…solo que es falso. Los efectos relativistas se notan solamente cuando comparamos con otros observadores. La persona que vive en el piso superior no nota que su reloj biológico adelanta, notara la diferencia cuando se encuentre con el vecino de abajo. Claro que la diferencia es tan pequeña que no la podemos apreciar.

Pues bien, estos efectos han sido medidos con instrumentos de increíble precisión. Pero ¿cómo funciona el efecto de la dilatación temporal de los relojes superiores?, el truco consiste en imaginar un fotón de luz que viaja de arriba hacia abajo, veamos como varia su energía a medida que desciende hasta la superficie terrestre.

Un fotón de energía hf, donde f es la frecuencia, también tiene una energía dada por la relación de Einstein mc². Así pues al fotón le podemos asociar una masa inerte m

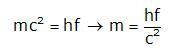
Pero esta es na masa relacionada con la inercia del fotón. ¿Tiene el fotón también una masa gravitatoria? La respuesta es sí, vean masa gravitatoria y masa inercial.

Según el principio de equivalencia la masa gravitatoria tiene el mismo valor que la masa inerte. Así pues, la energía electromagnética se convierte en masa inerte, que no podemos distinguir de la masa gravitatoria. Dicho de otro modo, un fotón dentro de un campo gravitatorio se comportará como si tuviese una masa dada por la ecuación anterior, aunque su masa en reposo sea cero.

Veamos con detalle que ocurre cuando un fotón de frecuencia f situado a una altura h de la superficie de la Tierra desciende hasta el suelo. A la altura h el fotón tiene una energía hf y una energía gravitatoria mgh. Al descender la energía gravitatoria se convierte en energía cinética y por tanto en energía que gana el fotón.

Cuando el fotón llega al suelo ha ganado la siguiente cantidad de energía. (Suponiendo que la masa se mantiene constante durante su caída)

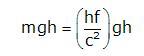
La energía total del fotón en el suelo (hf’) será la que tenía más la que ha ganado,

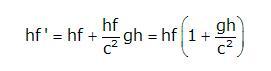
De esta manera observamos que la frecuencia del fotón ha aumentado ligeramente, en la cantidad siguiente.

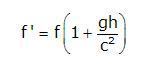
Observamos que el fotón de luz en su viaje a la superficie terrestre aumenta su frecuencia y disminuye su longitud de onda, como se puede apreciar en la siguiente figura.

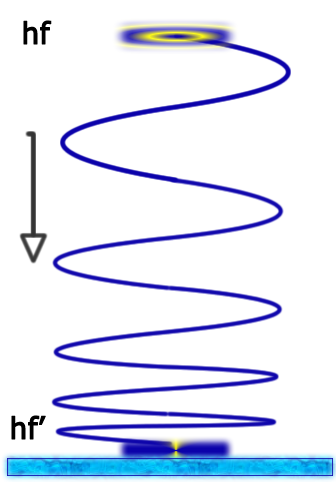
La variación relativa de la frecuencia del fotón se expresa mediante la siguiente ecuación.

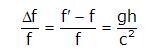
Se conoce también por desplazamiento al azul debido a la gravedad, ya que la frecuencia aumenta y por tanto disminuye la longitud de onda. La longitud de onda baja del espectro visible tiene color azul, en cambio una de elevada tiene color rojo, de ahí este nombre.  Si el fotón en lugar de caer ascendiera, observaríamos un desplazamiento al rojo.

Supongamos un fotón que cae desde una altura h de 20 metros, el desplazamiento al rojo será de

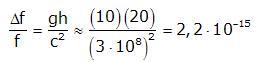
Es un efecto muy pequeño y por tanto muy difícil de observar. Pound y Rebka en el año 1960 midieron el efecto empleando una fuente de rayos gamma.

Seguimos suponiendo, ¿y si el fotón procediese de un reloj atómico situado a una distancia h de la superficie terrestre? ¿Y si lo comparamos con otro reloj idéntico situado en la superficie terrestre? ¿Funcionarían al mismo ritmo?La respuesta como he dicho antes,  es parecida a la paradoja de los mellizos.

Para responder la pregunta tenemos que comparar los dos relojes y para hacerlo tenemos que observarlos desde un sistema de referencia inercial. Escogemos el sistema de referencia del reloj situado en la superficie de la Tierra, donde el potencial gravitatorio es cero.

Observaremos que los fotones procedentes del reloj atómico superior tiene una frecuencia más elevada. Esto significa más vibraciones por segundo, es decir, más tic-tacs. Observamos que el reloj superior avanza más rápido. Es el efecto de la dilatación temporal en la paradoja de los mellizos.

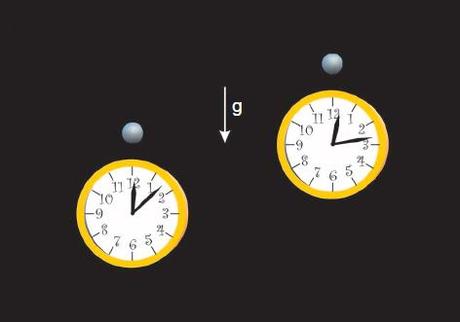
Science 329, 1630 (2010). Chou

Como he dicho antes, si dos relojes idénticos se separan de la superficie terrestre una altura de 1 kilometro, el reloj superior adelantaría tres segundos en un millón de años. Es decir 0,0003 segundos a lo largo de una vida.  Es un efecto muy pequeño, pero medible con la tecnología actual. Esto es lo que hizo el equipo de C.W. Chou.