Teorema de equivalencia (recta y curva)

                                 TEOREMA DE EQUIVALENCIA (RECTA - CURVA)

Teorema: La magnitud de una curva en un ángulo de  90º/ㄫ es igual a la magnitud del cateto menor de un triangulo rectángulo.

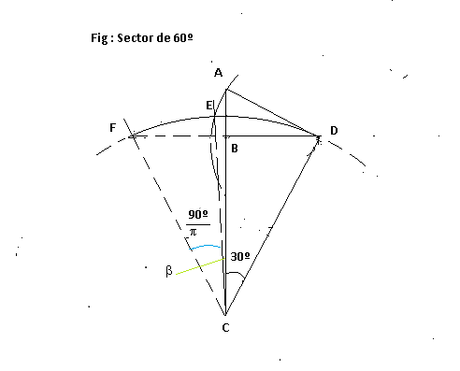
La prueba la haremos con la siguiente figura. En ella hemos trazados dos arcos de radios CD y AD los cuales tienen el punto de intersección en E, siendo el punto que limita a la curva FE cuya longitud es el segmento BD.

Aplicaremos únicamente la matemática simple: La ley de proporcionalidad.                                              

                      360º / nº  = 2πr / L

Por tanto tenemos 

                FD = L   ;  n = 60º

                FD =  60º* 2π*DC / 360º = ㄫ* DC / 3

A su vez

         ED =  2ㄫ*DC (30º + 𝛽) / 360º =  ㄫ*DC (30º + 𝛽) / 180º

Con lo cual

      EF = FD - ED

     EF = ㄫ* DC / 3  -  [ㄫ*DC (30º + 𝛽) / 180º]  =  ㄫ*DC (30º -  𝛽) / 180º

Definido el valor de EF,  por el teorema tenemos que: EF = DC/2

con lo cual  

            ㄫ*DC (30º -  𝛽) / 180º  = DC /2

Dividiendo  por DC tenemos 

                  ㄫ (30º -  𝛽) / 180º  = 1 / 2

es decir

              ㄫ (30º -  𝛽) / 90º   = 1

Con esta conoceremos el valor de   𝛽 y a su vez el ángulo (90º / ㄫ) reflejado en la figura.

También viene a decirnos que para que se cumpla el teorema el ángulo a de ser 90º/ㄫ. Esto lo he demostrado en el artículo publicado (IJMC VOL 28 (2) 2017 ; Titulo: The relationship between the angle (angular and the angle of the  tread) in a Cycloid and his transcendence). Aunque por derechos de autor  no pueda desarrollarlo aquí,  si puedo indicar que el ángulo de 90º/ㄫ, es el menor de los ángulos de un triangulo rectángulo de lados (a;2a) por consiguiente la tangente es 1/2 y el coseno 2/✓5.

Por tanto si en la figura trazamos desde cualquier punto de lado FE una perpendicular a él  hasta insertar en el lado EC tendremos  triángulos rectángulo de lados (a;2a).

Por primera vez, el mundo matemático conoce la magnitud de una curva en su línea recta.