Teorema de rolle y teorema del valor medio de lagrange

Teorema de Rolle
El teorema de Rolle dice lo siguiente:
Si:
f es una función continua definida en un intervalo cerrado [a,b]
f es derivable sobre el intervalo abierto (a,b)
f(a) = f(b)

Entonces: existe al menos un punto c perteneciente al intervalo (a,b) tal que f’(c) = 0.

En palabras más sencillas, si una curva regular sale y llega a la misma altura, en algún punto tendrá tangente horizontal.
En la figura se ven tres casos distintos. Si la función empieza subiendo, tendrá luego que bajar para reencontrar su valor inicial, entre la subida y la bajada, hay un punto donde la función alcanza un máximo, y en éste, f ‘ se anula. Lo mismo sucede si la función empieza bajando, y f ‘ es nula en el mínimo de f. El tercer ejemplo muestra que no se garantiza la unicidad de c.

Prueba

Gracias a la continuidad de f, la imagen de [a, b], conjunto conexo es un conjunto conexo de R, y por lo tanto es un intervalo, el intervalo imagen.
La imagen por una función continua de un conjunto compacto es un conjunto compacto, y por lo tanto el intervalo imagen es cerrado y de longitud finita: es de la forma [m, M], con m el valor mínimo de f y M su valor máximo.
Si m = M , la función es constante, y cualquier punto c de (a, b) conviene. Descartado este caso, m ≠ M significa que uno de los dos no es igual a F(x) = f(x). Supongamos que sea M. Entonces M > F(x) = f(x), y por lo tanto el máximo M está alcanzado en el interior del intervalo (corresponde al primer ejemplo).
Sea c en [a, b] tal que f(c) = M. Por definición del máximo, M = f(c) ≥ f(x) para todo x de [a, b]. Entoces el cociente (F(x) – f(x)) / (c – x) es no negativo cuando x c (el denominador se vuelve negativo no nulo). Pero f ‘(c) es por definición el límite de este cociente cuando x tiende hacia c. El límite por la izquierda, f ‘(c-)positivo, tiene que ser igual al límite por la derecha, f ‘(c+). Por lo tanto este límite común es nulo, o sea f ‘(c) = 0.
La prueba es muy parecida si es el mínimo que está alcanzado en (a, b).

Otra forma
De manera similar se puede considerar la siguiente prueba. Se sabe que existen tres posibilidades: o bien la función que consideramos es constante, o bien tiene algún punto x donde el valor de la función es mayor o bien este valor es menor que en los extremos. Para el primer caso es trivial que en algún punto la función tiene derivada nula (en la definición de derivada el cociente incremental es cero).
Para el segundo caso se puede probar lo siguiente:
Consideramos A como el conjunto imagen de f. Sabemos que A es un compacto ya que es la imágen de una función continua en un compacto y por lo tanto la función alcanza máximo evaluada en un punto x0 dentro del intervalo. Por ser la función derivable en (a,b), la función es derivable también en x0.
Aproximamos entonces a la función en un entorno del punto x0 considerando la derivada de f, f’(x). Entonces tenemos que si la derivada es positiva, entonces hay un entorno a la derecha de x0 en donde los valores de f(x) son mayores a f(x0), lo cual es absurdo por ser f(x0) = M el máximo del conjunto imagen.
De manera análoga, si la derivada fuera negativa tendríamos un entorno a la izquierda de x0 en donde los valores de f(x) son mayores a f(x0), lo cual es absurdo por ser f(x0) = M el máximo del conjunto imagen.
La única posibilidad que resta es que la derivada sea nula, lo cual demuestra el teorema de Rolle.
Basta tomar g(x) = -f(-x) y repetir la prueba para verificar que se verifica también cuando la función toma algún valor por debajo de los valores funcionales de los extremos.
[editar]Teorema de Valor Medio, de Lagrange o de Incrementos Fini

Teorema del valor medio.
Si:
f es una función continua definida en un intervalo [a, b]
f es derivable sobre el intervalo (a, b)
Entonces: existe al menos un punto c en el intervalo (a, b) tal que :

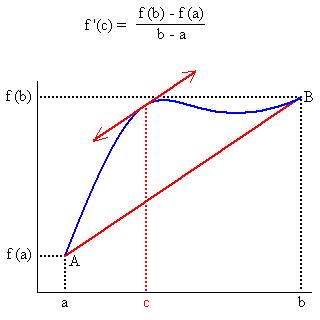
Es decir que existe un punto en donde la tangente es paralela a la cuerda AB.
Su prueba es sencilla, pues utiliza el teorema precedente.
Sea p la pendiente de la cuerda: p = (f(b) – f(a)) / (b – a), y se define la función g(x) = f(x) – p·x. Entonces g(b) – g(a) = f(b) – p·b – (f(a) – p·a) = f(b) – f(a) – p(b – a) = f(b) – f(a) -(f(b) – f(a)) = 0, y g como f, es continua sobre [a, b] y derivable en su interior.
Según el teorema anterior, existe un c en (a, b) tal que g ‘(c) = 0; pero esto se escribe f ‘ (c) = p.

Este teorema se escribe también, con las mismas hipótesis: f(b) = f(a) + f ‘(c)(b-a) lo que deja entrever el teorema de Taylor-Young:
f(b) = f(a) + (b-a)f ‘(a) + … + (b-a)n/n! · f(n)(c), con f n veces derivable sobre (a, b).